Вопрос 13

Уравнение плоскости с нормальным вектором.

Пусть в пространстве плоскость Q задана точкой ( ) и вектор =(А;В;С), перпендикулярным этой плоскости. Выведем уравнение плоскости Q. Возьмем на ней произвольную точку М(x;y;z) и составим вектор

=(х- ;у- ;z- )

При любом расположении точки М на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю.

А(х- )+В(у- ) +С(z- )=0

Координаты любой точки плоскости Q удовлетворяют уравнению.

Это уравнение называется уравнением плоскости, проходящей через данную точку =(х- ;у- ;z- ) перпендикулярно вектору =(А;В;С). Вектор =(А;В;С) называется нормальным вектором плоскости.

Вопрос 9.

Общее уравнение плоскости.

Рассмотрим общее уравнение первой степени с тремя переменными x,y,z.

Ах+Ву+Сz + D=0(1 уравнение)

Пологая, что по крайней мере один из коэффициентов А,В или С не равен нулю, например B≠0, перепишем уравнение в виде

А(х-0)+В +С(z-0)=0(2 уравнение)

Сравнивая (2) уравнение с уравнением плоскости, проходящей через данную точку =(х- ;у- ;z- ) перпендикулярно вектору =(А;В;С). Видим, что (1) и (2) уравнение являются уравнением плоскости с нормальным вектором =(А;В;С), проходящей через точку .

Итак, уравнение (1) определяет в системе координат некоторую плоскость. Уравнение (1) называется общим уравнением плоскости.

Вопрос10.

Взаимное расположение двух прямых.

Векторы, лежащие на одной или параллельных прямых называются коллинеарными. Нулевой вектор коллинеарин всем векторам.

Векторы называются комплонарными если они лежат на одной или параллельных плоскостях или если существует плоскость, которой они параллельны.

Два вектора называются, одинаково направлены (сонаправленые) если они коллинеарные и при сведении их начальных точек в одну точку, концы будут направлены в одну сторону.

Вопрос 11.

Расстояние от точки до прямой в

Пусть заданы прямая L равнением Ax+By+C=0 и точка ( )(рис). Требуется найти расстояние от точки до прямой L.

Решение. ( ), М€L=> её координаты удовлетворяют уравнению L

A +B +C=0=> =

Найдя координаты точки, мы можем найти d= *М (это перпендикуляр из М на L),как проекцию М* на прямую ⍊ L.

Пусть =(А;В) нормаль прямой L, тогда он будет являться направляющем вектором для прямой перпендикулярной L.

d= = => => =>

Так же точка € L и ранее мы нашли ёё координаты, то подставив её в при последнее записанное выражение, получим последнее равенство.

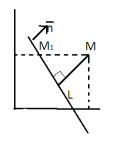
Вопрос 12.

Расстояние от точки до плоскости

Пусть задана точка ( ) и плоскость Q своим уравнением Ах+Ву+Сz + D=0. Расстояние d от точки до плоскости Q находится по формуле

d=

Расстояние d от точки до плоскости Q равна модулю проекции вектора , где ( ) – произвольная точка плоскости Q, на направление нормального вектора =(А;В;С)=>

d= = = =>

Так как точка ( ) принадлежит Q, то +D=0, т.е. D=

=> d=