64. Проверка отклонения распред-я вероятностей от норм-го распределения (гост р исо 5479-2002) – вероятностная бумага

Кумулятивную ф-цию распред-я наблюденных зн-ний строят на бумаге для норм-х вероятностных графиков. Вертик. ось имеет нелин-ю шкалу, соответствующую площади под стандартной ф-цией норм. распред-я и размечена знач-ми кумулят-ой относит-ой частоты. Другая ось имеет линейную шкалу для упорядоченных зн-ний х. Если кумулятив. Ф-ция распред-я переменной х приближ-ся к прямой линии, то распр-е переменной х будет норм-е.

Иногда эти оси меняют местами. Если выполнено нормирование переменной _х, лин-ю шкалу можно заменить логариф-ой, квадратич-ой, обратной или другой шкалой.

По вертикальной оси зн-ния кумулятив. относит-ой частоты даны в процентах, а по гориз-ой - произвольная линейная шкала.

Если график на этой бумаге представлен набором точек, кот. рассеянны около прямой линии, то это дает первое подтверждение утверждению, что ген.сов-сть, из кот. взята выборка, подчин-ся норм. закону распр-я. Этот подход важен тем, что дает наглядную инф-цию по типу отклонения от норм-го распр-я. Если график показ., что данные подчинены другому распр-ию, не имеющему отношения к норм., то в некот. случаях к норм.распред-ию можно перейти с помощью спец-го преобр-я. Если график показывает, что данные не подчин-ся простому однородному распр-ю, а скорее всего принадлежат смеси двух или нескольких однородных, то рекоменд-ся выявить подсовокупности и анализ каждой из них проводить отдельно.

Графич-я процедура состоит в расположении наблюденных зн-ний ( ) в неубывающем порядке и затем в нанесении значений вероятности , рассчитанных по ф-ле: на бумагу для нормальных вероят-х графиков (где _k – порядк-й номер _x; _{k= 1…n}).

График серии наблюдений на бумаге для нормальных вероятностных графиков

65. Проверка отклонения распред-я вероятностей от норм-го распред-я (гост р исо 5479-2002) – многонаправленный критерий ( )

Альтернатив. гипотеза состоит в следующем: распред-ие вероятностей имеет асимметрию, отличную от нуля, и (или) кривизна отлична от кривизны, свойственной норм-му распр-ю (без указания направления каждого отклонения). Альтернатив. гипотеза имеет один из видов:

Каждое из сочетаний , или , , или , может быть выбрано на равных основаниях. Тест многонаправленный и предназначен выявить сочетание ненулевой асимметрии и (или) кривизны .

Данный совместный критерий из-за выбора статистики нельзя считать многосторонним критерием в строгом смысле. Статистика этого критерия образована парой значений статистик ,

где 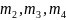- моменты 2го, 3го и 4го порядков соотв-но: , среднее арифм-е или момент 1го порядка рассчит-ют по ф-ле

 При нулевой гипотезе нормальности можно построить область вокруг точки (0; 3), в которую точка ( ) попадает с вероятностью р (с осями координат ). Кривые, ограничивающие эту область, показаны на рисунке при р=0,95 и рисунке 9b) при p =0,99 для различных объемов выборки _n.

При уровне значимости _{α =1-p} критическая область критерия образована точками, лежащими вне кривой, соответствующей объему выборки _n.