27 Билет.

1. Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0.

Если отрезок   является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по

1. Формуле левых прямоугольников: 

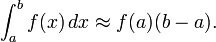
2. Формуле правых прямоугольников: 

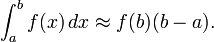
3. Формуле прямоугольников (средних): 

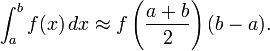
Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Метод парабол (метод Симпсона)

Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид

.

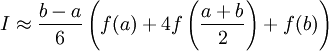Если разбить интервал интегрирования на   равных частей, то имеем

где  .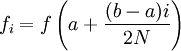

2. 13₁₆ , получится 2 тетрады переводим 1₁₆=0001₂ и 3₁₆=0011_{2 ,} убираем незначащие 0, получаем Ответ: 10011₂

0,1101₂ ; имеется 1 тетрада 1101, переводим по табл., получаем Ответ: 0,D₁₆

28 Билет.

1 . Метод Ньютона. Задан отрезок [а,Ь], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,Ь], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(X0)*F"(X0)>0). В точке F(х₀) строится касательная к кривой у= F(х) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:

2. первое 0,847*2=1,694(1) |

0,694*2=1,388(1) |

0,488*2=0,776(0) |

0,776*2=1,552(1) |=>

0,847₁₀=0,1101₂

Второе 0,0010101₂ допишем не значащий 0, получим 0,00101010₂ , в итоге получилось 2 тетрады

0010 и 1010

0010₂=2₁₆

1010₂=А₁₆

Ответ: 0,2А₁₆

29 Билет.

1. Алгоритм - это последовательность инструкций для выполнения какого либо задания.

Свойства алгоритма:

ДИСКРЕТНОСТЬ – разделение выполнения решения задачи на отдельные операции

ОПРЕДЕЛЕННОСТЬ (точность) алгоритма – определение однозначных действий исполнителя

ПОНЯТНОСТЬ – не должен быть рассчитан на принятие каких-либо самостоятельных решений

РЕЗУЛЬТАТИВНОСТЬ (конечность) алгоритма – исполнение алгоритма должно закончиться за конечное число шагов

ФОРМЫ ЗАПИСИ АЛГОРИТМОВ

v ЗАПИСАН НА ЕСТЕСТВЕННОМ ЯЗЫКЕ;

v ИЗОБРАЖЕН В ВИДЕ БЛОК СХЕМЫ;

v ЗАПИСАН НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ.

Анализ скорости выполнения алгоритмов

Производительность алгоритма можно оценить по порядку величины. Алгоритм имеет сложность порядка O(f(N)) (произносится «О большое от F от N»), если с увеличением размерности исходных данных N время выполнения алгоритма растет пропорционально функции f(N).

Сложность рекурсивных алгоритмов

Рекурсивными процедурами (recursive procedure) называются процедуры, вызывающие сами себя

2. первое 0,847*16=13,552(D)

0,552*16=8,832(8)

0,832*16=13,312(D)

0,D8D

Второе 0,0010101₂ допишем не значащий 0, получим 0,00101010₂ , в итоге получилось 2 тетрады

0010 и 1010

0010₂=2₁₆

1010₂=А₁₆

Ответ: 0,2А₁₆