26 Билет.

1.Интерполяция является частным случаем аппроксимации. Это - задача о нахождении такой аналитической функции L(x), которая принимает в точках (узлах) х_i заданные значения у_i. Иными словами, аппроксимирующая функция в случае интерполяции обязательно проходит через заданные точки.

Интерполяционная функция L(x) приближенно заменяет исходную f(x), заданную таблично, и проходит через все заданные точки – узлы интерполяции.

В связи с интерполяцией рассматриваются три основные проблемы:

1.Выбор интерполяционной функции L(x) .

2.Оценка погрешности интерполяции R(x).

3.Размещение узлов интерполяции для обеспечения наивысшей возможной точности восстановления функции

Чаще всего в качестве интерполяционной функции используется полином n-степени (полиноминальная функция)

Это объясняется тем, что полином n-степени, содержащий n+1 параметр и проходящий через все заданные точки – единственный.

Метод наименьших квадратов. В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины. В этом общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки. Рассмотри рисунок, отражающий большой разброс точек. В простейшем случае будем искать аппроксимирующую функцию ϕ(x) в виде полинома первой степени (прямой) ϕ(x) = a0 + a1x. Т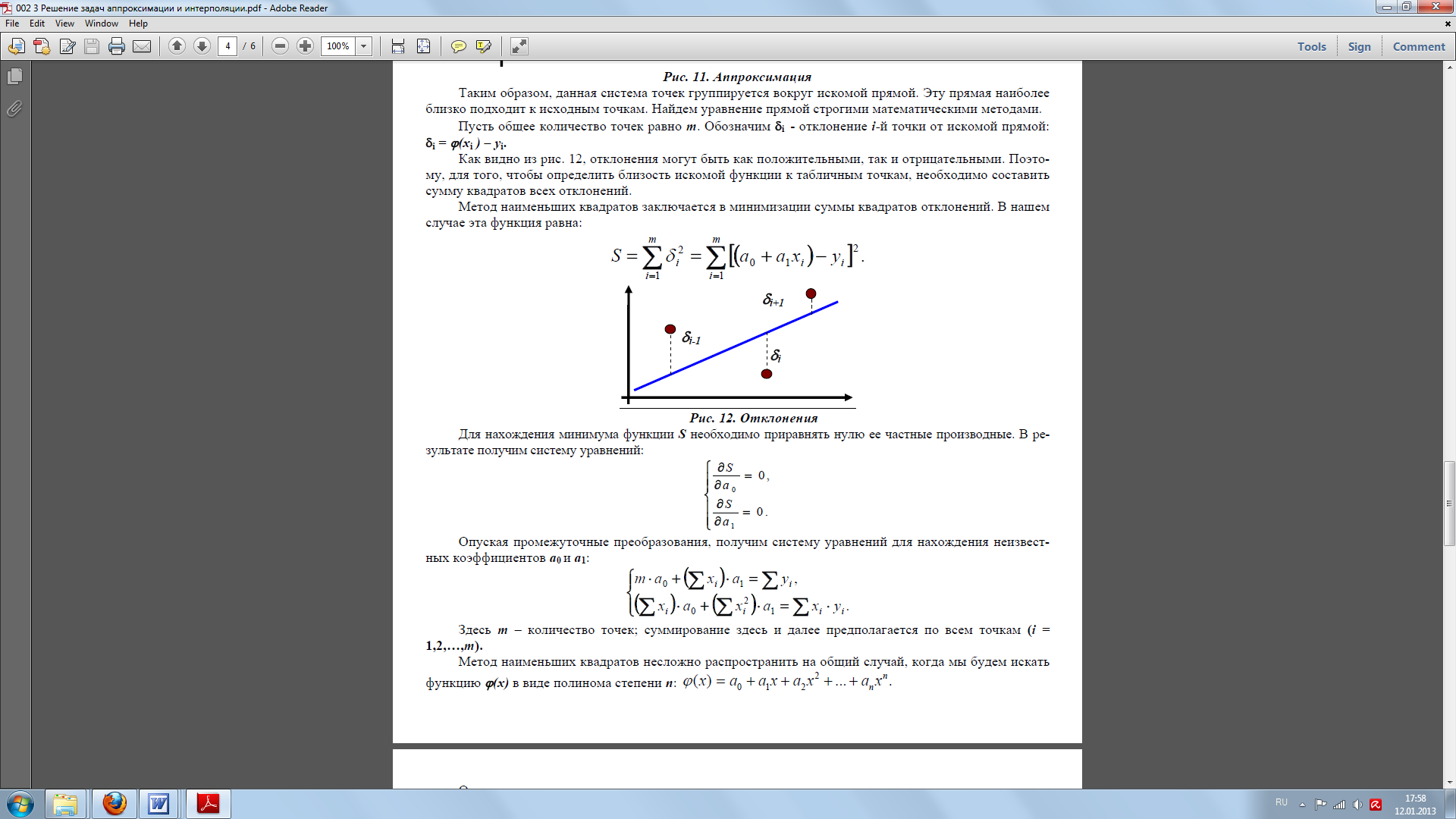 аким образом, данная система точек группируется вокруг искомой прямой. Эту прямая наиболее близко подходит к исходным точкам. Найдем уравнение прямой строгими математическими методами. Пусть общее количество точек равно m. Обозначим δi - отклонение i-й точки от искомой прямой: δi = ϕ(xi ) – yi. Как видно из рис., отклонения могут быть как положительными, так и отрицательными. Поэтому, для того, чтобы определить близость искомой функции к табличным точкам, необходимо составить сумму квадратов всех отклонений. Метод наименьших квадратов заключается в минимизации суммы квадратов отклонений. В нашем случае эта функция равна: Для нахождения минимума функции S необходимо приравнять нулю ее частные производные. В результате получим систему уравнений:

Опуская промежуточные преобразования, получим систему уравнений для нахождения неизвестных коэффициентов a0 и a1:

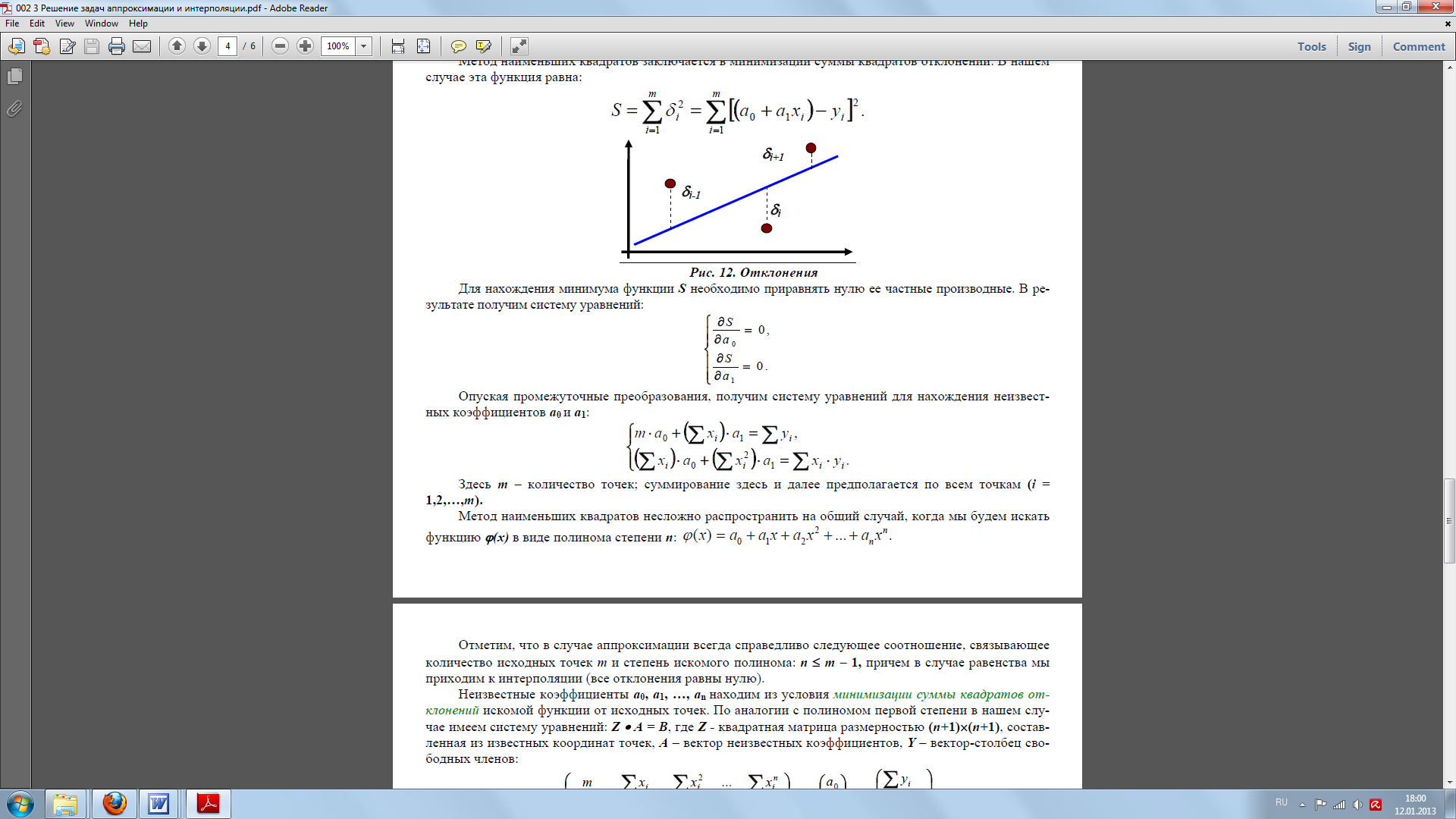
Здесь m – количество точек; суммирование здесь и далее предполагается по всем точкам (i =1,2,…,m). Метод наименьших квадратов несложно распространить на общий случай, когда мы будем искать функцию ϕ(x) в виде полинома степени n:ϕ(x) = a0 + a1 x + a2 x^2 +… + an x^n.Отметим, что в случае аппроксимации всегда справедливо следующее соотношение, связывающее количество исходных точек m и степень искомого полинома: n ≤ m – 1, причем в случае равенства мы приходим к интерполяции (все отклонения равны нулю).

2.

10011₂ допишем не значащие 00010011₂ , получаем 2 тетрады 0001 и 0011, переводим по табл., получаем Ответ:13₁₆

0,1101₂ ; имеется 1 тетрада 1101, переводим по табл., получаем Ответ: 0,D₁₆