21 Билет.

1. Метод половинного деления. Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность ε. Пусть задан отрезок [a,b], содержащий один корень уравнения.

Алгоритм метода:

1. Определить новое приближение корня x в середине отрезка [a,b]: x=(a+b)/2.

2. Найти значения функции в точках a и x: F(a) и F(x).

3. Проверить условие F(a)*F(x)<0. Если условие выполнено, то корень расположен на отрезке [a,x]. В этом случае необходимо точку b переместить в точку x (b=x). Если условие не выполнено, то корень расположен на отрезке [x,b]. В этом случае необходимо точку a переместить в точку x (a=x).

4. Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до тех пор, пока не будет выполнено условие |F(x)|<ε.

пример ручной реализации метода. Дано уравнение x^2 – 4x + 3 = 0. Известно, что единственный корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом половинного деления с точностью ε = 0,01. Построим таблицу в соответствии с алгоритмом метода. Алгоритм остановлен, поскольку |-0,00624|<0,01.Ответ: уточненное значение корня x ≈ 1,0031. Достоинство метода: более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [a,b] содержится более одного корня, то метод не работает.

2.

0,847*16=13,552(D)

0,552*16=8,832(8)

0,832*16=13,312(D)

Ответ: 0,D8D₁₆

22 Билет.

1. Метод Ньютона. Задан отрезок [а,Ь], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,Ь], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(X0)*F"(X0)>0). В точке F(х₀) строится касательная к кривой у= F(х) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:

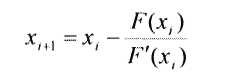
2.

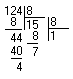Ответ: 174₁₀

174₁₀=1*8^2+7*8^1+4*8^0=124

0,D8D₁₆=13*16^(-1)+8*16^(-2)+13*16^(-3)= ~0,847

23 Билет.

1. Реализация численных методов состоит из двух этапов: 1) отыскание приближенного значения корня или содержащего его отрезка; 2) уточнение приближенного значения корня.

1 . Неустранимая погрешность. Она связана с тем, что параметрами математической модели служат обычно приближенные величины из-за принципиальной невозможности выполнения абсолютно точных измерений. Для вычислителя погрешность математической модели следует считать неустранимой (безусловной), хотя постановщик задачи иногда может ее изменить.

2. Погрешность метода. Это погрешность, связанная со способом решения поставленной математической задачи и появляющаяся в результате подмены исходной математической модели другой или конечной последовательностью других, например, линейных моделей.

3. Вычислительная погрешность (погрешность действий). Этот тип погрешности обусловлен необходимостью выполнять арифметические операции над числами, усеченными до количества разрядов, зависящего от применяемой вычислительной техники , вычислительная погрешность обусловлена округлениями.

Все три описанных типа погрешностей в сумме дают полную погрешность результата решения задачи. (Полная версия в 19 билете!)

Дискретная модель математической задачи представляет собой систему большого, но конечного числа алгебраических уравнений. Чем точнее мы хотим получить решение, тем больше уравнений необходимо взять. Говорят, что численный метод сходится, если при неограниченном увеличении числа уравнений решение дискретной задачи стремится к решению исходной задачи. Реальный ПК может оперировать лишь с конечным числом уравнений, на практике сходимость, как правило, не достигается. Поэтому важно уметь оценивать погрешность метода в зависимости от числа уравнений, составляющих дискретную модель. По этой причине дискретную модель строят таким образом, чтобы она правильно отражала качественное поведение решения исходной задачи даже при сравнительно небольшом числе уравнений. Сходимость численного метода тесно связана с его корректностью. Например, исходная математическая задача поставлена корректно, т.е. ее решение существует, единственно и непрерывно зависит от входных данных. Тогда дискретная модель этой задачи должна быть построена таким образом, чтобы свойство корректности сохранилось. В понятие корыстности численного метода включаются свойства однозначной разрешимости соответствующей системы уравнений и ее устойчивости по входным данным. Под устойчивостью понимается непрерывная зависимость решения от входных данных, равномерная относительно числа уравнений, составляющих дискретную модель.

2. первое 10101001,10111₂ Допишем не значащие нули, получаем 10101001,10111000₂

Всего получилось 4 тетрады 1010 1001 1011 1000

По табличным значениям!

1010₂ = A₁₆

1001₂ = 9₁₆

1011₂ = B₁₆

1000₂ = 8₁₆

Ответ:A9,B8₁₆

Второе 0,0010101₂ допишем не значащий 0, получим 0,00101010₂ , в итоге получилось 2 тетрады

0010 и 1010

0010₂=2₁₆

1010₂=А₁₆

Ответ: 0,2А₁₆