Глава 2. Числовые выборочные характеристики
2.1. Средние величины
1. а) Среднее арифметическое вариационного ряда – это сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот
=
Очевидно, что
=
,
где - относительные частоты.
Основные свойства средней арифметической
1) Средняя арифметическая постоянной равна самой постоянной.
2) Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз.
=
3) Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число
=
+с
4) Средняя арифметическая отклонений вариантов от средней арифметической равна нулю
=0
5) Средняя арифметическая суммы нескольких признаков равна сумме средних арифметических этих признаков
=
+
б) Средняя степенная к-го порядка
=
,
где хi>0
в) Средняя гармоническая
=
г) Средняя гармоническая
=
2. Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного вариационного ряда наблюдений.
Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов:
Ме=
Для группированной выборки (интервального ряда) медиана – это точка, в которой площадь гистограммы делится пополам.
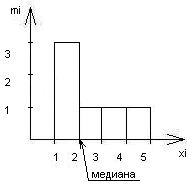
Рис. 2.1.
3. Модой Мо вариационного ряда называется варианта, которой соответствует наибольшая частота.
2.2. Показатели вариации
Средние величины не отображают изменчивости (вариации) значений признака.
1. Вариационный размах R равен разности между наибольшим и наименьшим вариантами ряда
R=xmax – xmin
2. Среднее линейное отклонение вариационного ряда – это средняя арифметическая абсолютных величин отклонений вариантов от их средней арифметической
d=
3. Дисперсией вариационного ряда S2 (Dв) называется среднее арифметическое квадратов отклонений вариантов от их средней арифметической
S2
=
Можно показать,
что S2
=
-(
)2
Основные свойства дисперсии
1) Дисперсия постоянной равна нулю.
2) Если все варианты увеличить (уменьшить) в одно и то же число к раз, то дисперсия увеличится (уменьшится) в к2 раз.
3) Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится.
4. Среднее квадратическое отклонение S (σ) – арифметическое значение корня квадратного из дисперсии
S=
5. Коэффициент вариации – процентное отклонение среднего квадратического отклонения к средней арифметической
V=
Для вычисления числовых характеристик выборки, заданной интервальной таблицей, эту таблицу заменяют на дискретную. В качестве принимаемых значений указывают середины интервалов группировки.
2.3. Начальные и центральные моменты вариационного ряда
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия – моментов вариационного ряда.
1. Начальный моментов к-го порядка вариационного ряда определяется по формуле
Vk=
Очевидно, что V1= , т.е. средняя арифметическая является начальным моментом первого порядка.
2. Центральный момент к-го порядка вариационного ряда определяется по формуле
μк=
Очевидно, что центральный момент второго порядка является дисперсией вариационного ряда.
3. Коэффициентом асимметрии вариационного ряда называется число
А=
Если А=0, то распределение имеет симметричную форму, т.е. варианты, равноудаленные от х имеют одинаковую частоту. При А>0 (А<0) говорят о положительной (правосторонней) или отрицательной (левосторонней) асимметрии.
4. Коэффициентом эксцесса вариационного ряда называется число
Е=
Эксцесс является показателем «крутости» вариационного ряда. Эксцесс нормально распределенной случайной величины равен нулю. Если Е>0 (Е<0), то полигон вариационного ряда имеет более крутую (пологую) вершину по сравнению с нормальной кривой.