32. Расстояние от точки до прямой.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + C = 0вычисляется по формуле: 

33. Линии второго порядка: окружность.

Определение. Линией (кривой) второго порядка называется линия общее уравнение которой имеет следующий вид:

 

.

 

Уравнение второй степени вида   (не содержащее члена   c произведением координат) называется пятичленным уравнением кривой второго порядка. Оно определяет на плоскости   эллипс, гиперболу и параболу (с возможными случаями распада и вырождения этих кривых) с осями симметрии, параллельными осям координат, в зависимости от знака произведения коэффициентов   и  . Окружность является простейшей кривой второго порядка.

Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки.

Уравнение окружности имеет вид

(x - a)² + (y - b)² = r²,

где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид

x² + y² = r².

34. Эллипс.

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a² - b² = c².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.

35. Гипербола.

Обратной пропорциональностью называют функцию, заданную формулой y = k/x где k неравно 0. Число k называется коэффициентом обратной пропорциональности.

Если считать х независимой переменной, а у — зависимой, то формула y = k/x определяет у как функцию от х. График функции y = k/x называют гиперболой.

Гипербола имеет две ветви, которые расположены в первом и третьем квадратах, если k > 0, и во втором и четвертом квадрантах, если k > 0.

Функция y = k/x , где k > 0 обладает следующими свойствами:

1. область определения функции — множество всех действительных чисел, за исключением числа

2. множество значений функции, все числа кроме числа 0

3. y = k/x — нечетная

4. принимает положительные значения при х > 0 и отрицательные — при x < 0

5. убывает на промежутках х < 0 и х > 0. Если k < 0, то функция y = k/x обладает свойствами 1—3, а свойства 4—5 формулируются так: принимает положительные значения при х < 0 и отрицательные при х > 0

6. возрастает на промежутках х < 0 и х > 0.

  Каноническое уравнение: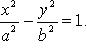 

36. Парабола.

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

        

Уравнение параболы

y = ax²+ bx + c