17. Векторы на плоскости и в пространстве.

Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также инулевой вектор, начало и конец которого совпадают.

• Длиной (модулем) вектора называется расстояние между началом и концом вектора.|АВ|=|а|

• Длина вектора в координатах определяется как расстояние между точками начала и конца вектора.

•  Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

• Два вектора называются равными, если они сонаправлены и их длины равны.

• Векторы называются ортогональными, если они перпендикулярны.

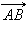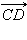• Если два ненулевых вектора   и   коллинеарны, а лучи AB и CD сонаправлены, то векторы   и   называются сонаправленными

• Два вектора называются противоположными, если их длины равны, и они противоположно направлены

  

Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:

Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам: Скалярным произведением  векторов  называется число:

18. n-мерный вектор и векторное пространство.

Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр. Методология данного раздела математики позволила подробно изучить такого рода структуру через призму одной из главных её характеристик — размерности векторного пространства. Размерность представляет собой максимальное число линейно независимых элементов пространства, то есть, прибегая к геометрической частности, число направлений, невыразимых друг через друга посредством только операций сложения и умножения на скаляр. Векторное пространство можно наделить дополнительными структурами, например, нормой или скалярным произведением.

Упорядоченная совокупность n действительных или комплексных чисел  называется n-мерным вектором. Числа   называются координатами вектора

Свойства операций над n-мерными векторами.

1. свойство коммутативности сложения векторов a + b = b + a;

2. свойство ассоциативности векторов (a + b) + c = a + (b + c);

3. существует нейтральный вектор по операции сложения, им является нулевой вектор, a + 0 = a;

4. для любого вектора существует противоположный вектор, которые в сумме дают нулевой вектор a + (-a) = 0;

5. Сочетательное свойство умножения  .

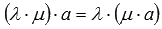6. Первое распределительное свойство  .

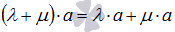7. Второе распределительное свойство  .

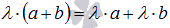8. существует нейтральное число по операции умножения, им является единица .

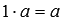19. Линейная комбинация векторов. Линейная зависимость и независимость векторов

 Линейная комбинация векторов 

     Линейной комбинацией векторов   называют вектор

     

где   - коэффициенты линейной комбинации. Если  комбинация называется тривиальной, если   - нетривиальной.

Если линейная комбинация   может представлять собой нулевой вектор тогда, когда среди чисел   есть хотя бы одно, отличное от нуля, то система векторов   называется линейно зависимой.

Если линейная комбинация   представляет собой нулевой вектор только тогда, когда все числа   равны нулю, то система векторов   называется линейно независимой.

Свойства линейно зависимых и линейно независимых векторов

1. Если в систему векторов входит нулевой вектор, то она линейно зависима

2. Если в системе векторов имеется два равных вектора, то она линейно зависима.

3. Если в системе векторов имеется два пропорциональных вектора  , то она линейно зависима.

4. Система из   векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.

5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.

6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.

7. Если система векторов   линейно независима, а после присоединения к ней вектора   оказывается линейно зависимой, то вектор   можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.