12. Матричная запись системы линейных уравнений.

  Матричная запись системы линейных уравнений 

AX = B,

где

13. Формулы Крамера.

Метод годиться только для квадратных матриц : число уравнений равно числу неизвестных.

Алгоритм решения

• Вычислить определитель

∆ = IАI ≠ 0

• Сконструировать для каждой переменной свои определитель

D _i (i= )

Теорема Крамера. Система n линейных уравнений с n неизвестными имеет единственное решение, если определитель системы не равен 0, и это решение находится по формуле Крамера:

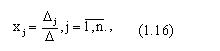
где определители D  называются определителями неизвестных х_j и получаются из главного определителя путем замены j-го столбца столбцом свободных членов.

14. Решение системы линейных алгебраических уравнений с помощью обратной матрицы.

метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу.

A * X = B |*(слева) A^-1

A^-1= A * X = A^-1*B

E * X = A^-1*B

X = A-1*B

15. Метод Гаусса.

Метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

Пример

На первом этапе нужно записать расширенную матрицу системы:

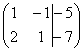
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: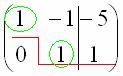 

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

Рассмотрим первое уравнение системы   и подставим в него уже известное значение «игрек»:

Ответ: 

16. Системы линейных однородных уравнений. Фундаментальная система решений. Однородной системой m линейных уравнений с n неизвестными называется система вида



      	a11x1 + a12x2 + … + a1nxn = 0 a21x1 + a22x2 + … + a2nxn = 0 … … … … … … … … … … … am1x1 + am2x2 + … + amnxn = 0

Эта система может быть записана в виде матричного уравнения

A · X = O

Система (1) имеет очевидное решение x₁⁰  =  x₂⁰  =   …   =  x_n⁰ = 0 тривиальное

 Для того, чтобы однородная система n линейных уравнений с n неизвестными (матрица системы A — квадратная) имела нетривиальное решение, необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю ( det  A = 0 ).

Любой базис пространства решений однородной системы линейных уравнений называется ундаментальной системой решений однородной системы.Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.