1. Основные сведения о матрицах. 2. Операции над матрицами. 3. Определители, их свойства. 4. Определители второго и третьего порядка. 5. Миноры, алгебраические дополнения. 6. Определители n-го порядка. 7. Методы вычисления определителей.  8. Обратная матрица. 9. Метод Жордана вычисления обратной матрицы. 10. Ранг матрицы.  11. Система линейных алгебраических уравнений. Основные понятия и определения. 12. Матричная запись системы линейных уравнений. 13. Формулы Крамера. 14. Решение системы линейных алгебраических уравнений с помощью обратной матрицы. 15. Метод Гаусса. 16. Системы линейных однородных уравнений. Фундаментальная система решений. 17. Векторы на плоскости и в пространстве. 18. n-мерный вектор и векторное пространство. 19. Линейная комбинация векторов. Линейная зависимость и независимость векторов. 20. Размерность и базис векторного пространства. 21. Переход к новому базису в векторном пространстве. 22. Евклидово пространство. 23. Базисы в евклидовом пространстве. 24. Линейные операторы. Определения, операции. 25. Зависимость между матрицами линейного оператора при переходе в другой базис. 26. Собственные векторы и собственные значения. 27. Квадратичные формы. Определение, канонический вид, ранг. 28. Знакоопределенность квадратичной формы. Критерии. 29. Уравнения линии на плоскости. 30. Различные виды уравнений прямой линии на плоскости. 31. Условия параллельности и перпендикулярности прямых на плоскости. 32. Расстояние от точки до прямой.  33. Линии второго порядка: окружность. 34. Эллипс. 35. Гипербола. 36. Парабола.  37. Уравнения плоскости в пространстве. 38. Уравнения прямой в пространстве. 39. Общая формулировка задачи линейного программирования. 40. Примеры задач линейного программирования.  41. Построение математической модели ЗЛП. 42. Графическое решение двумерных задач линейного программирования.

1. Основные сведения о матрицах. Матрица - таблица чисел, содержащая m строк и n столбцов, размера m · n. Числа m и n определяют размер матрицы.

Числа (функции или алгебраические выражения) a_ij - элементы матрицы; i - номер строки (i = 1, 2, ..., m); j - номер столбца (j = 1, 2, ..., n).

• Если m ≠ n - матрица прямоугольная.

• Две матрицы A и B одинакового размера называются равными ,если они совпадают поэлементно.

• Матрица, в которой число строк равно числу столбцов (m = n), называется квадратной.

• Матрица размера 1 · n(имеющая одну строку) - матрица-строка.

• Матрица размера m · 1(имеющая один столбец) - матрица-столбец.

• Матрица, все элементы которой равны нулю (a_ij = 0), называется нулевой.( обознач. O)

• К 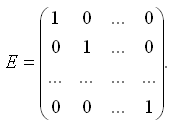вадратная матрица, в которой все недиагональные элементы 0 называется диагональной (обознач.D).

• Квадратная матрица, на главной диагонали которой находятся только единицы называется единичной (обознач. I или E):

• Квадратная матрица, элементы которой симметричны относительно главной диагонали называется симметричной.

• Квадратная матрица, элементы которой находятся выше/ниже главной диагонали называется треугольной

• матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю называется ступенчатой

2. Операции над матрицами.

1. Операция сложения матриц. Возможна только для матриц одного размера. Тоесть

А + В = С

А_mxn=(a_ij); B_mxn=(b_ij)

C_mxn=A + B= C_ij

C_ij= a_{ij +} b_{ij , где ij – любые числа}

Свойства операции сложения матриц.

1. Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А + (В + С) = (А + В) + С.

2. Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А + О = А.

3. Для ненулевой матрицы А данного порядка существует матрица ( – А ), их суммой является нулевая матрица: А + ( - А ) = О.

4. Для матриц А и В данного порядка справедливо свойство коммутативности сложения А + В = В + А.

2. Операция умножение матриц Операция умножения двух матриц А и В определена, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.

A_mxk * B_kxn= C_mxn

свойства операции умножения матриц.

1. Свойство ассоциативности умножения матриц  .

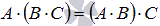2. Два свойства дистрибутивности 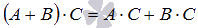  и  .

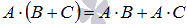3. В общем случае операция умножения матриц некоммутативна  .

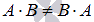4. Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо 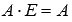 , а для произвольной матрицыА порядка n на p справедливо  .

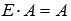3. Умножения матриц на число

B = α * A

B_ij = α * a_ij, где ij – любые числа

Свойства операции умножения матрицы на число.

1. Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа   справедливо свойство дистрибутивности  .

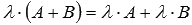2. Для произвольной матрицы А и любых действительных (или комплексных) чисел   и 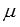 выполняется свойство дистрибутивности .

3. Для произвольной матрицы А и любых действительных (или комплексных) чисел   и  справедливо свойство ассоциативности умножения  .

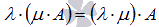4. Нейтральным числом по умножению на произвольную матрицу А является единица, то есть,  .

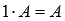4. Вычитание

D= B – A= B + (-1)*A

5. Деление на число

6. Деление матриц

3. Определители, их свойства.

Определи́тель (или детермина́нт) является многочленом от элементов квадратной матрицы. Существует только для квадратных матриц.  Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Свойства определителя

• Определитель изменит только знак если поменять 2 строки местами.

• Если определитель имеет 2 одинаковых строки, то он равны нулю

• Определитель можно раскрывать по эл-там любой строки

• Если в определителе имеется нулевая строка, то он равен нулю

• Общий множитель любой строки определителя можно вынести за его знак

• Если в определителе есть 2 пропорциональные строки, то он равен нулю

• Если к эл-там некоторой строки прибавить эл-ты другой его строки, умноженной на одинаковое число, то определитель не изменится

• Если матрицу транспонировать, то определитель не изменится

• Все свойства справедливы и для столбцов

4. Определители второго и третьего порядка.

Определитель второго порядка равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали.

Определителем квадратной матрицы второго порядка (или просто определителем второго порядка) называется число, равное a11a22 - a12a21.

a 11 a12

A =

a21 a22

Определители третьего порядка.

Определителем квадратной матрицы третьего порядка (или просто определителем третьего порядка)

называется число, равное a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32:

a11 a12 a13

A= a21 a22 a23

a31 a32 a33

Правило треугольников

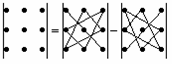
Со знаком плюс берется произведение элементов, образующих главную диагональ, а также элементов, образующих равнобедренные треугольники с основаниями, параллельными главной диагонали; со знаком минус — произведение элементов, образующих побочную диагональ, а также элементов, образующих равнобедренные треугольники с основаниями, параллельными побочной диагонали.