1.6. Проверка гипотезы о нормальном распределении случайной величины по критерию Пирсона

Для проверки гипотезы о нормальном распределении случайной величины X сравним между собой экспериментальные и теоретические частоты по критерию Пирсона:

Критерий Пирсона определяет меру расхождения между выборочными данными и теоретическими, определяемыми в соответствии с высказанной гипотезой о распределении случайной величины Х. Если экспериментальные вероятности совпадут с теоретическими , то значение равно нулю.

Чем ближе значение к нулю, тем с большей вероятностью можно будет принять гипотезу о предполагаемом распределении.

Статистика имеет распределение с 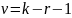степенями свободы, где число k - число интервалов вариационного ряда, r - число параметров теоретического распределения. Число параметров нормального распределения равно двум , следовательно, число степеней свободы равно .

В теории математической статистики доказывается, что проверку гипотезы о модели закона распределения по критерию Пирсона можно делать только в том случае, если выполняются следующие условия:

где .

Из результатов вычислений, приведенных в Табл. 8, следует, что необходимое условие для применения критерия согласия Пирсона не выполнено, так как в некоторых группах . Поэтому те группы вариационного ряда, для которых необходимое условие не выполняется, объединяют с соседними и уменьшают число групп; при этом частоты объединенных групп суммируются. Так объединяют все группы с частотами до тех пор, пока для каждой новой группы не будет выполняться условие:

.

При уменьшении числа групп для теоретических частот соответственно уменьшают и число групп для эмпирических частот. После объединения групп в формуле для числа степеней свободы , где в качестве k принимают новое число групп, полученное после объединения частот.

Результаты объединения интервалов и теоретических частот приведены в Табл. 9.

Таблица 9.

Результаты объединения интервалов и теоретических частот

[хi-1; хi)	piT	niT	ni	(ni-niT)2
[3,7844; 5,0225)	0,1611	9,6660	9	0,4436	0,0459
[5,0225; 5.6415)	0,2181	13,0869	16	8,4862	0,6484
[5.6415; 6,2605)	0,2461	14,7655	16	1,5240	0,1032
[6,2605; 6,8796)	0,1725	10,3494	8	5,5197	0,5333
[6,8796; 8,7367)	0,1006	6,0346	11	24,6552	4,0856
Σ	0,8984	53,9024	60		5,4165

Результаты вычислений из Табл. 9. можно использовать для проверки гипотезы о нормальном распределении с помощью критерия Пирсона.

Процедура проверки гипотезы о нормальном распределении случайной величины X выполняется в следующей последовательности:

1. Зададимся уровнем значимости 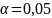или одним из следующих значений: ; ; .

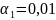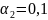2. Вычислим наблюдаемое значение критерия:

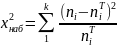
используя экспериментальные и теоретические частоты из Табл. 9.

3. Для выбранного уровня значимости по таблице распределения находим критические значения при числе степеней свободы , где k - число групп экспериментального распределения.

4. Сравним фактически наблюдаемое значение с критическим значением , найденным по Табл. 4., и примем одно из следующих решений:

а) если , то выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдений при заданном уровне значимости, т.е. нет оснований отвергать гипотезу о нормальном распределении, так как эмпирические и теоретические частоты различаются незначительно;

б) если , то выдвинутая гипотеза о теоретическом законе распределения отвергается при заданном уровне значимости.

При выбранном уровне значимости и числе групп k = 5 число степеней свободы v = 2, по Табл. 4. для и v = 2 находим

В результате получим:

для 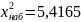, которое найдём по результатам вычислений, приведенных в Табл. 9, имеем:

Следовательно, выдвинутая гипотеза о теоретическом законе распределения не противоречит выборке наблюдения при заданном уровне значимости и нет оснований отвергать гипотезу о нормальном распределении случайной величины.