университет
кино и телевидения
Министерство культуры российской федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КИНО И ТЕЛЕВИДЕНИЯ»
Институт Экономики и Управления
Кафедра информационного менеджмента и бухгалтерского учёта.
КУРСОВОЙ ПРОЕКТ
По дисциплине «Статистика»
на тему: «Статистическая обработка данных.
Расчет аналитических показателей ряда динамики.
Статистика рынка труда»
Вариант 12.
Выполнил:
Студентка 042 группы ФаУ
Пешкина К.А.
Руководитель:
доц. Волчанинов В.В
Санкт-Петербург
2012
Содержание
Введение ………...…………………………………………….…………………..3
1. Статистическая обработка данных ……………...……………………………4
Постановка задачи. Цель работы. Исходные данные ……………...……4
Вычисление основных выборочных характеристик по заданной выборке ………………………………………………………………...…...5
Результаты вычисления интервальных оценок для математического ожидания и дисперсии ……………………………………………...…......8
Результаты ранжирования выборочных данных и вычисление моды и медианы ………………………………………………………………...…...13
Параметрическая оценка функции плотности распределения ………....16
Проверка гипотезы о нормальном распределении случайной величины по критерию Пирсона ………………………………………....................25
2. Ряды динамики. Аналитические показатели ряда динамики. Пример расчётов……………………………….………………………………………….28
2.1. Классификация рядов динамики…………..………………………….28
2.2. Аналитические показатели изменения уровней ряда динамики……30
3.Статистика рынка труда……………………………………………………….39
3.1. Экономически активное население………………………………….39
3.2.Трудовые ресурсы, методы расчета численности трудовых ресурсов…………………………………………………………………………..42
3.3. Коэффициент занятости………….……………………………………47
3.4.Понятие и виды безработицы………………………………………..49
3.5.Коэффициент безработицы…………………………………………..53
Библиография………………………………………………………………….....56
Введение
Статистика – это самостоятельная общественная наука, которая изучает количественную сторону массовых явлений и процессов, исследует закономерности общественного развития в конкретных условиях, места и времени.
Многовековая и древняя история статистики (от латинского слова status - «состояние и положение вещей») свидетельствует о крайней важности существования данной науки.
Актуальность работы вызвана тем, что в наше время важность правильной, рациональной организации и реализации статистических методов вошла в повседневный обиход современной жизни. Это неудивительно. Статистика является корреляционной наукой. Она включает в себя разделы как теоретические, так и прикладные (экономическая, социальная, отраслевая статистика). В этой связи статистика представляет собой необходимое звено в системе организации и функционирования, как малого субъекта бизнеса, так и страны в целом.
Курсовая работа состоит из двух глав. Первая глава призвана обеспечить анализ количественной стороны массовых явлений, служит основой для принятия соответствующих управленческих решений. Также в данной главе рассматривается определение функции плотности и построение ее графика, сравнение экспериментальной и теоретической вероятности. Вторая глава раскрывает понятие рынка труда, в ней рассмотрены основные категории трудоспособного и экономически активного населения, рассмотрены коэффициенты, с помощью которых и определяется количественная оценка социальных явления.
Целью курсового проекта является изучение и усвоение основных понятий математической статистики, овладение методикой статистического оценивания числовых характеристик случайной величины и нормального закона распределения, знакомство с методикой применения статистических критериев для проверки гипотез.
1. Статистическая обработка данных
1.1. Постановка задачи. Цель работы. Исходные данные.
Постановка задачи:
По выборке объёма n провести статистическую обработку результатов выборочных наблюдений (статистических наблюдений).
Цель работы:
изучить и усвоить основные понятия дисциплины "Статистика";
овладеть методикой статистического оценивания числовых характеристик случайной величины и нормального закона распределения;
ознакомиться с методикой применения статистических критериев для проверки гипотез.
Пусть проведено выборочное исследование (эксперимент) и имеются выборочные значения объёма n=60, которые представляют собой реализацию случайной величины Х.
Исходные данные представлены в Табл. 1.
Таблица 1.
Исходные данные
5.3274 |
5.0976 |
5.8452 |
6.9472 |
7.5504 |
6.4290 |
5.4392 |
6.1793 |
5.2285 |
5.0566 |
4.5924 |
4.0939 |
5.9347 |
6.6721 |
6.2061 |
5.9919 |
6.0200 |
5.4416 |
7.8861 |
5.7800 |
4.5856 |
5.6972 |
5.4304 |
5.8785 |
5.6098 |
5.1557 |
4.2622 |
5.5505 |
4.4521 |
5.9042 |
6.9077 |
8.3696 |
6.5198 |
6.4105 |
7.0526 |
6.4288 |
7.2951 |
5.8139 |
6.1307 |
5.3424 |
5.2407 |
5.4048 |
6.8124 |
6.0695 |
4.1663 |
7.8274 |
6.6541 |
4.4552 |
5.6249 |
6.2077 |
5.2344 |
5.8936 |
6.3388 |
7.0335 |
4.5952 |
4.9694 |
5.3566 |
6.1708 |
7.3448 |
7.9363 |
|
|
|
|
1.2. Вычисление основных выборочных характеристик по заданной выборке.
Для расчета основных числовых характеристик выборочных наблюдений составим таблицу (Табл. 2).
Таблица 2
i |
Показатель |
|
|
|
|
1 |
5,3274 |
0,6035 |
0,3642 |
-0,2198 |
0,1326 |
2 |
5,2285 |
0,7024 |
0,4933 |
-0,3465 |
0,2434 |
3 |
6,0200 |
0,0891 |
0,0079 |
0,0007 |
0,0001 |
4 |
5,6098 |
0,3211 |
0,1031 |
-0,0331 |
0,0106 |
5 |
6,5198 |
0,5889 |
0,3468 |
0,2043 |
0,1203 |
6 |
5,2407 |
0,6902 |
0,4764 |
-0,3288 |
0,2269 |
7 |
5,6249 |
0,3060 |
0,0936 |
-0,0286 |
0,0088 |
8 |
5,3566 |
0,5743 |
0,3298 |
-0,1894 |
0,1088 |
9 |
5,0976 |
0,8333 |
0,6944 |
-0,5786 |
0,4821 |
10 |
5,0566 |
0,8743 |
0,7644 |
-0,6683 |
0,5843 |
11 |
5,4416 |
0,4893 |
0,2394 |
-0,1171 |
0,0573 |
12 |
5,1557 |
0,7752 |
0,6009 |
-0,4658 |
0,3611 |
13 |
6,4105 |
0,4796 |
0,2300 |
0,1103 |
0,0529 |
14 |
5,4048 |
0,5261 |
0,2768 |
-0,1456 |
0,0766 |
15 |
6,2077 |
0,2768 |
0,0766 |
0,0212 |
0,0059 |
16 |
6,1708 |
0,2399 |
0,0576 |
0,0138 |
0,0033 |
17 |
5,8452 |
0,0857 |
0,0073 |
-0,0006 |
0,0001 |
18 |
4,5924 |
1,3385 |
1,7915 |
-2,3979 |
3,2096 |
19 |
7,8861 |
1,9552 |
3,8229 |
7,4746 |
14,6144 |
20 |
4,2622 |
1,6687 |
2,7845 |
-4,6464 |
7,7534 |
21 |
7,0526 |
1,1217 |
1,2583 |
1,4114 |
1,5832 |
22 |
6,8124 |
0,8815 |
0,7771 |
0,6850 |
0,6038 |
23 |
5,2344 |
0,6965 |
0,4851 |
-0,3379 |
0,2353 |
24 |
7,3448 |
1,4139 |
1,9992 |
2,8267 |
3,9967 |
25 |
6,9472 |
1,0163 |
1,0329 |
1,0498 |
1,0669 |
26 |
4,0939 |
1,8370 |
3,3745 |
-6,1989 |
11,3873 |
27 |
5,7800 |
0,1509 |
0,0228 |
-0,0034 |
0,0005 |
28 |
5,5505 |
0,3804 |
0,1447 |
-0,0550 |
0,0209 |
29 |
6,4288 |
0,4979 |
0,2479 |
0,1234 |
0,0615 |
30 |
6,0695 |
0,1386 |
0,0192 |
0,0027 |
0,0004 |
31 |
5,8936 |
0,0373 |
0,0014 |
-0,0001 |
0,0000 |
32 |
7,9363 |
2,0054 |
4,0217 |
8,0652 |
16,1741 |
33 |
7,5504 |
1,6195 |
2,6228 |
4,2477 |
6,8793 |
34 |
5,9347 |
0,0038 |
0,0000 |
0,0000 |
0,0000 |
35 |
4,5856 |
1,3453 |
1,8098 |
-2,4347 |
3,2753 |
36 |
4,4521 |
1,4788 |
2,1868 |
-3,2338 |
4,7821 |
37 |
7,2951 |
1,3642 |
1,8611 |
2,5389 |
3,4637 |
38 |
4,1663 |
1,7646 |
3,1137 |
-5,4945 |
9,6954 |
39 |
6,3388 |
0,4079 |
0,1664 |
0,0679 |
0,0277 |
40 |
6,4290 |
0,4981 |
0,2481 |
0,1236 |
0,0616 |
41 |
6,6721 |
0,7412 |
0,5494 |
0,4072 |
0,3018 |
42 |
5,6972 |
0,2337 |
0,0546 |
-0,0128 |
0,0030 |
43 |
5,9042 |
0,0267 |
0,0007 |
0,0000 |
0,0000 |
44 |
5,8139 |
0,1170 |
0,0137 |
-0,0016 |
0,0002 |
45 |
7,8274 |
1,8965 |
3,5968 |
6,8214 |
12,9368 |
46 |
7,0335 |
1,1026 |
1,2158 |
1,3405 |
1,4781 |
47 |
5,4392 |
0,4917 |
0,2418 |
-0,1189 |
0,0584 |
48 |
6,2061 |
0,2752 |
0,0757 |
0,0208 |
0,0057 |
49 |
5,4304 |
0,5005 |
0,2505 |
-0,1254 |
0,0627 |
50 |
6,9077 |
0,9768 |
0,9542 |
0,9321 |
0,9104 |
51 |
6,1307 |
0,1998 |
0,0399 |
0,0080 |
0,0016 |
52 |
6,6541 |
0,7232 |
0,5230 |
0,3783 |
0,2736 |
53 |
4,5952 |
1,3357 |
1,7840 |
-2,3829 |
3,1828 |
54 |
6,1793 |
0,2484 |
0,0617 |
0,0153 |
0,0038 |
55 |
5,9919 |
0,0610 |
0,0037 |
0,0002 |
0,0000 |
56 |
5,8785 |
0,0524 |
0,0027 |
-0,0001 |
0,0000 |
57 |
8,3696 |
2,4387 |
5,9473 |
14,5039 |
35,3709 |
58 |
5,3424 |
0,5885 |
0,3463 |
-0,2038 |
0,1199 |
59 |
4,4552 |
1,4757 |
2,1776 |
-3,2135 |
4,7421 |
60 |
4,9694 |
0,9615 |
0,9244 |
-0,8888 |
0,8546 |
Итого |
355,8529 |
46,5244 |
57,7189 |
18,5223 |
151,6747 |
Среднее арифметическое случайной величины Х :
Среднее линейное отклонение:
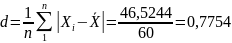
Смещённая оценка дисперсии случайной величины Х :
Несмещённая оценка дисперсии случайной величины Х :
Смещённое среднее квадратическое отклонение:
Несмещённое среднее квадратическое отклонение:
Коэффициент вариации:
Коэффициент асимметрии случайной величины Х :
9. Коэффициент эксцесса случайной величины Х :
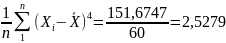
10. Вариационный размах:
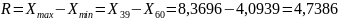
На основании полученных вычислений можно сделать следующие выводы:
Необходимое условие V< 33% для того, чтобы выборка имела нормальный закон распределения, выполняется:
V
=
%
<
33%.
Для нормального распределения коэффициенты асимметрии и эксцесса должны быть равны нулю
Выборочный коэффициент асимметрии служит для характеристики асимметрии распределения случайной величины. Если распределение симметрично относительно математического ожидания (среднее значение), то коэффициент асимметрии равен 0.
Для
выборочных распределений, как
правило, коэффициент асимметрии отличен
от нуля. Асимметрия положительна, если
длинная часть кривой распределения
расположена справа от математического
ожидания. Асимметрия отрицательна, если
длинная часть кривой расположена слева
от математического ожидания. Если кривая
плотности распределения симметрична,
имеет одну вершину, то среднее значение
,
мода
и
медиана
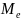совпадают.
По результатам вычислений асимметрия близка к нулю
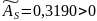
Это означает, что длинная часть функции плотности расположена справа от математического ожидания.
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой.
Если эксцесс положительный, то кривая имеет более высокую и острую вершину, чем нормальная кривая. Если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и плоскую вершину, чем нормальная.
Коэффициент
эксцесса равен
.
Он отрицательный,
а это значит что сравниваемая кривая
имеет более низкую и плоскую вершину,
чем нормальная.