10. Модифицированный метод суперпозиции
Оказывается при реализации метода суперпозиции можно ограничиться одним случайным числом γ.
В
отличие от алгоритма метода суперпозиции
вместо числа розыгрыша
можно
использовать число η
, которое можно рассчитать с помощью
числа
и
коэффициентов разложения
Пример.
Пусть
необходимо получить значения случайной
величины с плотностью распределения
вероятности
для
(закон
Релея в оптике или угловое распределение
фотонов в комптоновском рассеянии) .
Представим p(x) в виде
где
.
тогда соответствующая функция распределения F(x) представима в виде суммы
(39)
где
Тогда процесс получения значений случайной величины с заданным интегральным законом распределения состоит в выполнении следующих шагов:
Разыгрываем номер как значение дискретной величины
(40)
используя число
Затем, получаем значение случайной величины из уравнений
,
если k=1
или
если
k=2,
используя число . В итоге имеем значение x случайной величины
25. Системы отсчета и моделирование характеристик процессов столкновений
Реакции
взаимодействия частиц изучают в
различных системах отсчета. Вдвухчастичном
процессе соударения сталкиваются две
частицы 1 и 2 с 4-импульсами
= (
,
)
и
= (
,
)
соответственно. Величины
и
обычно фиксированы условиями эксперимента
в пределахошибок измерения. Система
отсчета определяется требованиями,
чтобы
или
имело
то
или иное значение. Чаще всего употребляются:
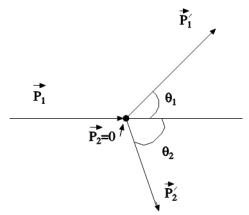
1.Лабораторная система (ЛС) – система, в которой проводится эксперимент и измеряются все энергии и импульсы. Это может быть либо система отсчета, в которой пучок частиц налетает на неподвижную мишень(см. рисунок 1): = 0 . (1)
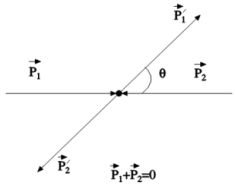
2. Система центра инерции (СЦИ) – система, в которой (см. рисунок 2):
+
= 0 (2). В результате столкновения частиц
могут рождаться новые частицы. Их
количество и состав определяются
законами сохранения и динамикой
взаимодействий. Наиболее простой случай
столкновения - это бинарные реакции:1
(
,
,
)
+ 2, (
,
,
)
→ 1’, (
,
,
)
+ 2’, (
,
,
)
(3).Рассмотрим основные кинематические
соотношения для бинарных реакций,
которые следуют из закона сохранения
4-импульса. Такие соотношения играют
важную роль при моделировании
характеристик вторичных частиц.
Рассмотрим для начала лабораторную
систему отсчета. Запишем систему для
импульсов и энергий частиц участвующих
втакого рода взаимодействиях:
=
+
(4),
+
=
+
(5).
Из закона сохранения энергии имеем,
что
=
−
−
(6),
т.е. для определения энергий
,
вторичных
частиц достаточно знать энергию однойиз
них (конечно мы считаем что характеристики
начальных частиц известны).
При моделировании характеристик процесса удобно ввести долю переданной энергииє:
є
=
/
+
(7),
для которой 0 < є< 1.Возводя в квадрат
уравнение (4) и учитывая, что
=
−
получаем:cos
=
−
−
−
+
+
/2
(8),где
=
+
- угол между частицами с импульсами
и
.
С помощьювышеизложенного способа
несложно рассчитать углы
.
И после аналогичных преобразований
получим:cos
=
−
−
−
+
+
/2
(9).
Как следует из соотношения (8), углы
разлета вторичных частиц в лабораторной
системе отсчета полностью определяются
массами покоя частиц реакции и энергиями
вторичных частиц и начальных частиц.
А с учетом соотношения (6) для вычисления
угловых характеристик достаточно
только значения энергии одной из
вторичных частиц.
Рассмотрим
основные кинематические соотношения
для бинарных реакций для системы центра
инерции.
+
=
0 =
+
(10),
+
=
+
(11).Используя уравнения (10),(11) несложно
найти, что энергии вторичных частиц
определяются
=
s
+
−
,
=
s
+
−
/2
(12),
где s
=
.Как
следует из соотношений (12), энергии
вторичных частиц в системе центра
инерции фиксируются массами покоя и
энергиями начальных частици следовательно
их не надо разыгрывать как случайные
величины. А угол меду частицами 1 и 1’θ
(см. рисунок 2) не фиксирован и может
находиться в пределах от 0 до π.
Второй угол φ,
который фиксирует направлениедвижения
частицы 1’ может принимать значения в
пределах 0 ≤ φ
≤ πс
равной вероятностью (при отсутствии поляризации).Углы, определяющие направление движения частицы 2’, как следуетиз рисунка 2 можно найти, если известны, сферические углы частицы 1’:θ’= π − θ , φ’= π + φ(13).