4.Сложение случайных чисел и центральная предельная теорема.

Пусть имеется N одинаковых независимых случайных величин , так что распределения вероятностей этих величин совпадают (они могут быть как дискретные, так и непрерывные). Значит их математические ожидания и дисперсии совпадают:

M = M = … =M = m

D = D =… = D = b²

Введем случайную величину p_N, которая является суммой случайных величин

p_N=

Так как для произвольных независимых случайных величин ξ и ν выполняются соотношения

M(ξ+ ν)=M ξ+M ν и D(ξ+ ν)=D ξ+D ν

то

M p_N=M( )=Nm

D p_N=D( )=N b²

Теорема: При больших N (т.е. при N→∞) случайная величина p_N описывается нормальным распределением с математическим ожиданием равным Nm и дисперсией D= N b²

т.е. плотность распределения

где a= Nm,

Следовательно, вероятность найти случайную величину p_N в пределах от α до β:

5. Розыгрыш дискретной случайной величины

Дискретная случайная величина χ, как правило, задается законом распределения в виде таблицы , где x₁, x₂, . . . , x_n - значения случайной величины χ, а p₁, p₂, . . . , p_n – вероятности появления этих значений. Другими словами Prob(χ = x_i) = p_i. Наша задача состоит в воспроизведении значений x₁, x₂, . . . , x_n случайной величины χ, с вероятностями появления равными p₁, p₂, . . . , p_n соответсвенно. Алгоритм розыгрыша дискретной случайной величины

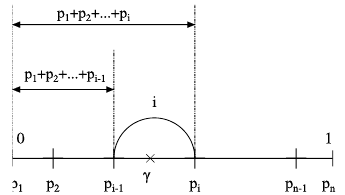
1. Необходимо разбить интервал (0,1) на n - интервалов, длины которых равны p₁, p₂, ..., p_n соответственно. 2. Разыгрываем значение стандартной случайной величины γ. 3. Проверяем условие попадания значения γ в i-тый интервал длинной p_i: p₁ + p₂ + . . . + p_i−1 < γ < p₁ + p₂ + . . . +p_i. Если неравенство верно, то приписываем случайной величине χ значение, соответствующее данному интервалу т.е. x_i. 4. При необходимости повторяем шаги 1 − 3 несколько раз с помощью

новых значений стандартной величины γ для получения других значений дискретной случайной величины с законом распределения вероятностей.На рисунке представлено графическая иллюстрация алгоритма розыгрыша дискретной величины. Для экономии времени выгодно расположить значения дискретной случайной величины x_i, так чтобы выполнялось соотношение p₁ < p₂ < ... < p_n.

6. Метод обратной функции

Метод обратной функции основан на теореме:

Если случайная величина ξ имеет плотность распределения вероятности p(x) > 0 на интервале (a, b) (a < x < b), то случайная величина ξ удовлетворяющая уравнению F(ξ) = γ (1), где F (x) функция распределения F(x) = , а γ стандартная равномерно распределенная величина наинтервале (0, 1) величина имеет плотность распределения p(x).

Как следует из этой теоремы, с помощью генератора случайных чисел γ уравнениеγ = F(x)

= (2)позволяет воспроизвести значения случайной величины ξ с плотностью распределенияp(x) на интервале (a, b) путем обращения(инверсии) уравнения (2):x = (γ) (3).

Такой метод получения называют методом обратной функции(или методом инверсии).