1.Компоненты компьютерного эксперимента.
Можно выделить следующие этапы разработки компьютерных моделей:
- постановка задачи моделирования (чёткое определение и формулировка цели разработки и дальнейших исследований; определяются зависимости, подлежащие изучению, а также основные факторы, характеризующие изучаемый объект и подлежащие учету при построении математической модели)
- построение математической модели(можно подразделить на стадии содержательного описания исследуемой системы и составления формализованной схемы математической модели)
- компьютерная реализация модели:
1.необходимо построить моделирующий алгоритм(представляется в виде логической схемы математической модели, содержащей математические формулы и уравнения, а также логические условия, отражающие последовательность математических вычислений, направления передачи данных, взаимодействия отдельных компонентов математической модели)
2. выбор языка и системы программирования
3. написание программы и её отладка
- исследование разработанной модели и ее корректировка (например, Если погрешность моделирования превышает установленные критерии (модель не адекватна), то проводится анализ причин возникновения погрешностей как в математической, так и в программной части модели, определяются пути повышения точности и осуществляется необходимая корректировка соответствующих блоков модели)
2.Интегральный закон распределения вероятностей.
Интегральным
законом, или функцией распределения
вероятностей
случайной величины Х, называют функцию,
значения которой для каждого
есть вероятность события, состоящего
в том, что случайная величина Х меньше
,
т.е.
(1)
График интегральной функции
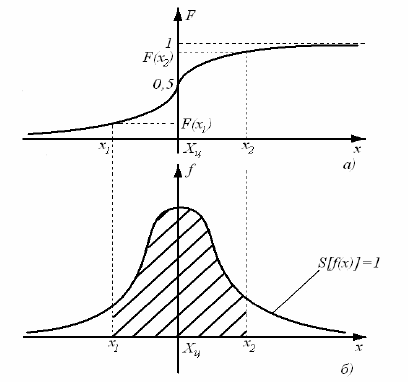
Она имеет следующие свойства:
− неотрицательная, т.е. F(x) ≥ 0;
− неубывающая, т.е. F (x2) ≥ F(x1), если x2 ≥ x1;
− диапазон ее изменения: от 0 до 1, т.е. F(−∞) = 0; F(+∞) = 1;
− вероятность нахождения случайной величины х в диапазоне от x1 до x2: P{x1 < x < x2}= F(x2) − F(x1).
3.Дифференциальный закон распределения вероятностей.
Для случайной величины с непрерывной и дифференцируемой функцией распределения F(x) можно найти дифференциальный закон распределения вероятностей. Он задается
(1)
p(x)называют кривой плотности распределения.
Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде
;
(2)
Если известен дифференциальный закон распределения p(x), то вероятность F попадания случайной величины х в интервал от x1 до x2 можно записать в следующем виде
Графически эта вероятность выражается отношением площади, лежащей под кривой f (x) в интервале от x1 до x2 к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [− ∞; + ∞] равна единице, т.е. представляет собой достоверное событие.