1 . Шкала электромагнитных волн

2.Типы оптических сред

Среду называют оптически анизотропной, если её оптические свойства (фазовая скорость света, показатель преломления) зависят от направления распространения световой волны и характера её поляризации.

Вакуум – идеальная модель для описания световых волн. (с=3*10Е8)

Изотропная – вещество рассматривается как совокупность заряженных частиц в вакууме, размещенных на расстоянии большем чем их размеры (среда в которой свойства одинаковы во всех направлениях).

Неоднородная- оптические св-ва меняются в зависимости от координаты.

3.Волновое уравнение

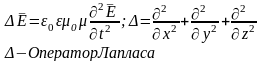
4.Плоские и сферические волны

Волна называется плоской, если векторы Е и Н зависят только от времени, и одной декартовой координаты.

Волна называется сферической, если её интенсивность зависит только от расстояния r до некоторой точки, называемым центром волны.

5. Вектор Пойтинга

Количество энергии, переносимой через единицу поверхности, перпендикулярной к направлению распространения энергии, за единицу времени, называется вектором Пойтинга (мгновенной плотностью потока энергии): Р=[ЕН];

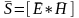
6. Интенсивность света

Модуль среднего по времени значения по плотности энергии, перенос световой волны.

Для любой электромагнитной волны: I=<ЕН>

Для световой волны:

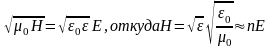
Значит интенсивность световой волны: I~nE². 7. Поляризация волны

В каждой точке поля плоской монохроматической волны конец вектора Е описывает эллипс, лежащий в плоскости yOz; уравнение этого эллипса имеет вид:

Такая волна называется эллиптически поляризованной.

Если a1=a2, то эллипс превращается в окружность и волна называется циркулярно поляризованной. Если al=0, или а2=0, то плоская волна называется линейно поляризованной (плоскоплояризованной).

8. Степень поляризации

Выражение - называется степенью поляризации

Imax,Imin – максимальная и минимальная интенсивности света, соответствующая двум взаимно перпендикулярным компонентам Е.

9. Закон Малюса

I=I_ocos²a, где: Io- интенсивность входящего света, k_n- коэффициент прозрачности анализатора, a - угол между плоскостями поляризации входящего света и света, пропускаемого анализатором. (a – угол между оптическими осями кристаллов (Io=1/2Iестеств.)

10.Условие возникновение интерференции. Когерентность колебаний. Для наблюдения интерференции, необходимо наличие двух и более когерентных колебаний, дающих биения с частотой, доступной для наблюдения.

Согласно принципу суперпозиции, полное световое поле, возникающее при наложении волн, равно их сумме. Результирующее поле существенно зависит от фазовых соотношений, которые оказываются различными в различных точках пространства. В некоторые точки пространства интерферирующие волны приходят в фазе и дают результирующее колебание с амплитудой, равной сумме амплитуд слагаемых а₁+а₂(имеется ввиду интерференция двух лучей); в других точках волны оказываются противофазными, и амплитуда результирующего колебания есть | a₁-a₂|. Интенсивность результирующего поля в первом случае оказывается равной Imax=( a₁+a₂)², во втором Imin=(a₁-a₂)², в то время как сумма интенсивностей есть I₁+I₁= а₁²+а₂².Таким образом, в первом случае Imax>I₁+l₂, во втором Imin<I₁+I₂.B тех точках пространства, в которых фазовый сдвиг отличен от 0 и p, реализуется некоторое промежуточное значение интенсивности Imin<I<Imax- мы получаем, таким образом, характерное для интерференции двух лучей плавное чередование светлых и темных полос. Волны называются когерентными, если разность фаз возбуждаемых волнами колебаний остаётся постоянной во времени

11. Комплексная степень когерентности

r₁₂(τ)= Г₁₂(r)/(√ r₁₁(0) √ r₂₂(0))= Г₁₂(r)/( √Г₁√I₂);

r₁₂(τ)=| Г₁₂(r)|exp[iv]; I(o)=I₁(p)+I₂(p)+2√I₁(p)I₂(p) Г₁₂(r)cos(δ)

12.Временная когерентность. Пространственная когерентность.

Если колебания, возбуждаемые волной в достаточно близких точках псевдоволновой поверхности, оказываются когерентными, то такая когерентность называется пространственной.

13.Длина и время когерентности.

Максимальное расстояние, на которое могут отстоять друг от друга две точки, колебания в которых остаются когерентными, называется длиной пространственной когерентности.

Время, за которое случайное изменение фазы волны достигает значения порядка я называется временем когерентности.

14.Двухлучевая интерференция. Деление фронта и деление амплитуды

Под двухлучевой интерференцией понимают интерференционную картину, возникающую

при сложении двух световых волн одинаковой частоты.

15.Полосы равного наклона и равной толщины.

Полосы равного наклона - интерференционная картина, имеющая вид системы светлых и тёмных круговых полос с общим центром, полученная на системе, состоящей

плоскопараллельной пластинки и линзы.

Полосы равной толщины — интерференционная картина, имеющая вид чередующихся светлых и тёмных полос, полученная на системе, состоящей из клина и линзы.

16.Просветление оптики. Условие просветления.

В просветленной оптике для устранения отражения света на каждую свободную поверхность линзы наносится тонкая пленка вещества с показателем преломления иным, чем у линзы. Толщина пленки подбирается так, чтобы волны, отраженные от обеих ее поверхностей, погашали друг друга. Особенно хороший результат достигается в том случае, если показатель преломления пленки равен корню квадратному из показателя преломления линзы. При этом условии интенсивность обеих отраженных от поверхностей пленки волн одинакова.

Условие просветления оптики-n₀<n₁<n₂: n₀-воздух, n₁-пленка, n₂-стекло

17. Схема интерферометра Фабри Перо.

18.Принцип Гюйгенса-Френеля.

Каждый элемент волновой поверхности служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента

19.3оны Френеля.

Зоны, построенные, что расстояния от краёв каждой зоны до любой точки Р отличаются на l/2 (l — длина волны в той среде, в которой распространяется волна), называются зонами Френе

л

.-. ..' ..- ..«-

20.Границы дифракционных приближений

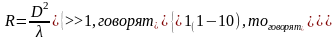
При m>>1 (сотни тысяч) дифракционные эффекты незначительны и описываются законами геометрической оптики (распределение интенсивности).

21.Угловая ширина дифракционного максимума при дифракции на щели

В случае, когда b>>l, значение sin(l/b) можно положить равным l/b. Тогда формула для угловой ширины центр, максимума:

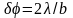
22.Дифракционная решётка

Совокупность большого числа одинаковых, отстоящих друг от друга на одно и тоже расстояние щелей. Расстояние d между серединами соседних щелей называется периодом решетки.

23.Условие главных максимумов для диф. решётки.

d sin j = ±ml, m=0,1,2,3... для перпендикулярного падения лучей d(sin j - sinq ) = ±ml, m=0,1,2,3... для лучей, падающих под углом

24.Угловая дисперсия и разрешающая сила решётки.

Угловая дисперсия: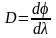 где 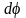- угловое расстояние между спектральными линиями, отличающиеся по длине dl.

Разрешающая сила: R=mN, где m- порядок спектра, N- число щелей

25.Критерий разрешения Рэлея

Два близких максимума воспринимаются раздельно, если середина одного максимума совпадает с краем другого.

2 6.Формулы Френеля для нормального падения света

27.Угол Брюстера

Угол, удовлетворяющий условию: tgq=n₁₂ называется углом Брюстера. При падении света под углом Брюстера отраженный и преломлённый лучи перпендикулярны.

28.Полное внутреннее отражение.

Явление, при котором световая волна проникает во вторую среду на расстояние порядка длины волны и затем возвращается в первую среду, называется полным внутренним отражением.

29.Оптическая ось кристалла

Оптической осью анизотропного кристалла в точке О называют прямую, проходящую через точку О перпендикулярно к плоскости кругового сечения оптической индикатрисы.

ИНДИКАТРИСА (франц. indicatrice, букв. — указывающий), в оптике — графическое изображение зависимости характеристик светового поля (яркости, поляризации света) или оптических характеристик среды (показателей преломления, отражательной способности) от направления.