- •Метод Зейделя
- •Погрешность произведения и частного
- •1) Метод зейделя
- •2)Погрешность произведения и частного
- •Метод левых прямоугольников
- •Погрешность суммы и разности
- •Метод итераций слу
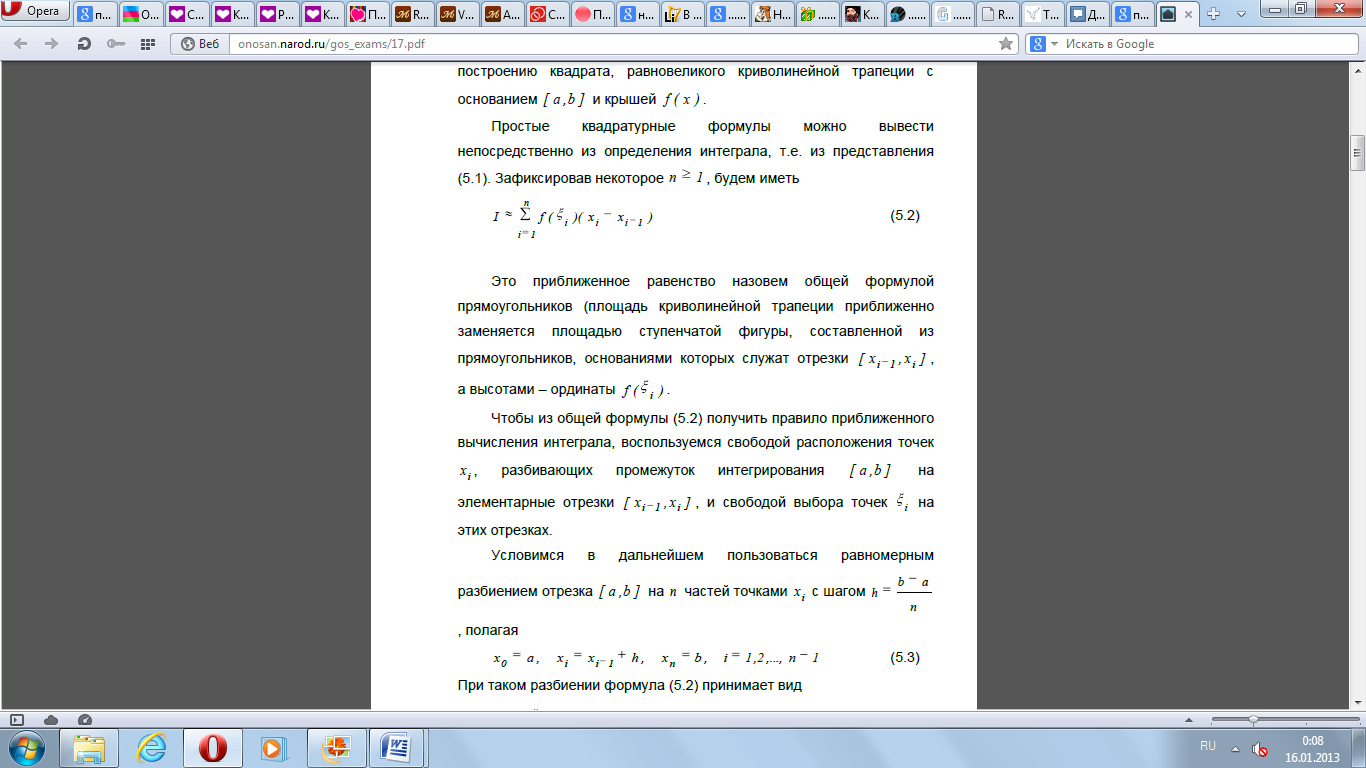
- •Постановка задачи численного интегрирования
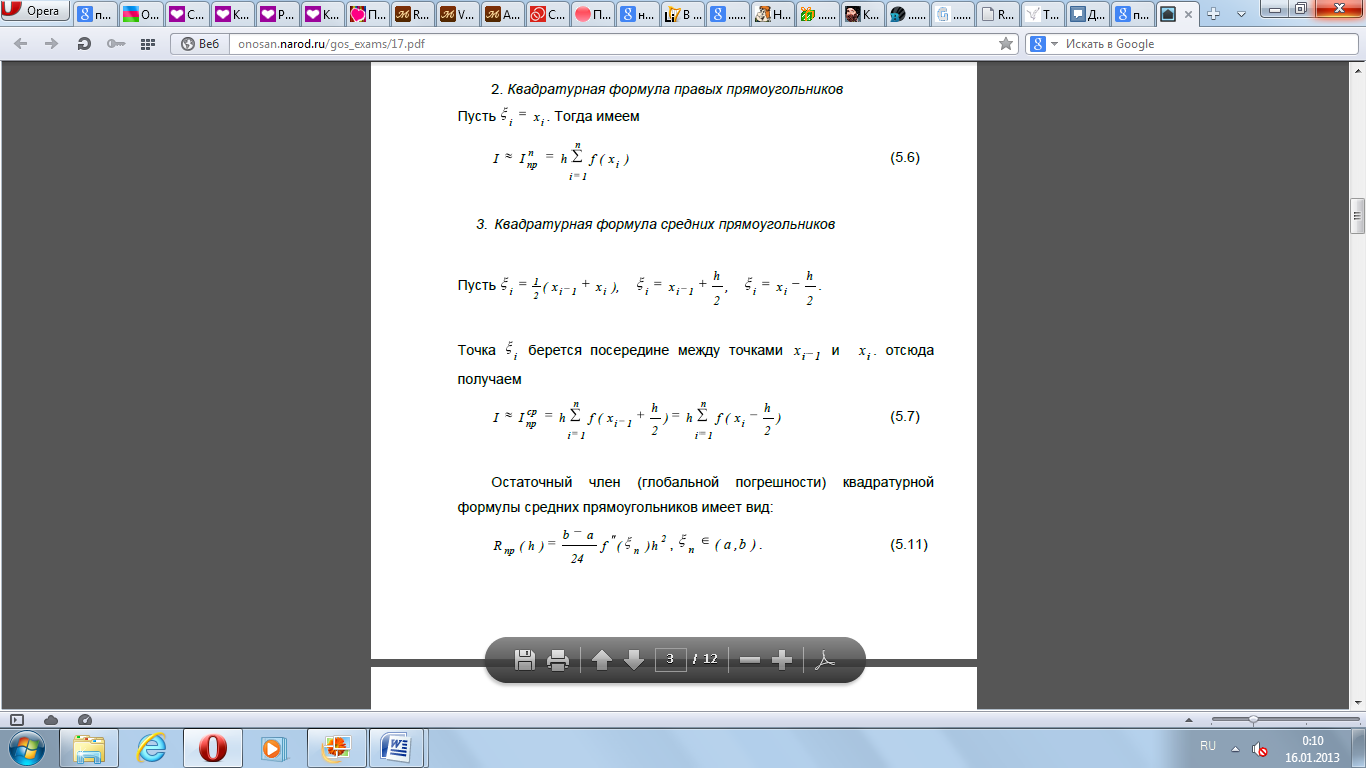
- •Метод правых прямоугольников
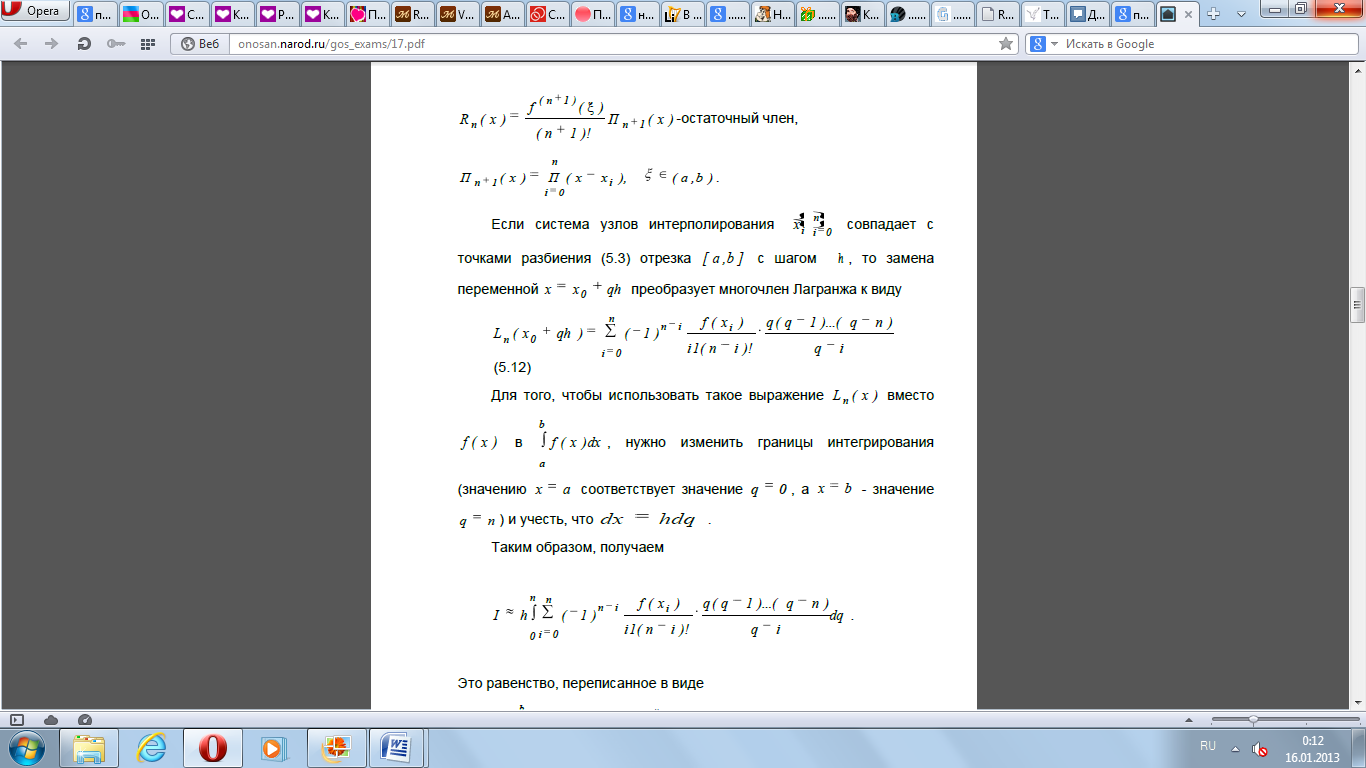
- •Интерполяционная формула Лагранжа
- •2) Лагранжа интерполяционная формула
- •Метод Гаусса
- •Метод Хорд
- •Метод правых прямоугольников
- •Метод касательных
- •Метод касательных.
- •Вопрос1
- •Вопрос 2
- •Метод проб.
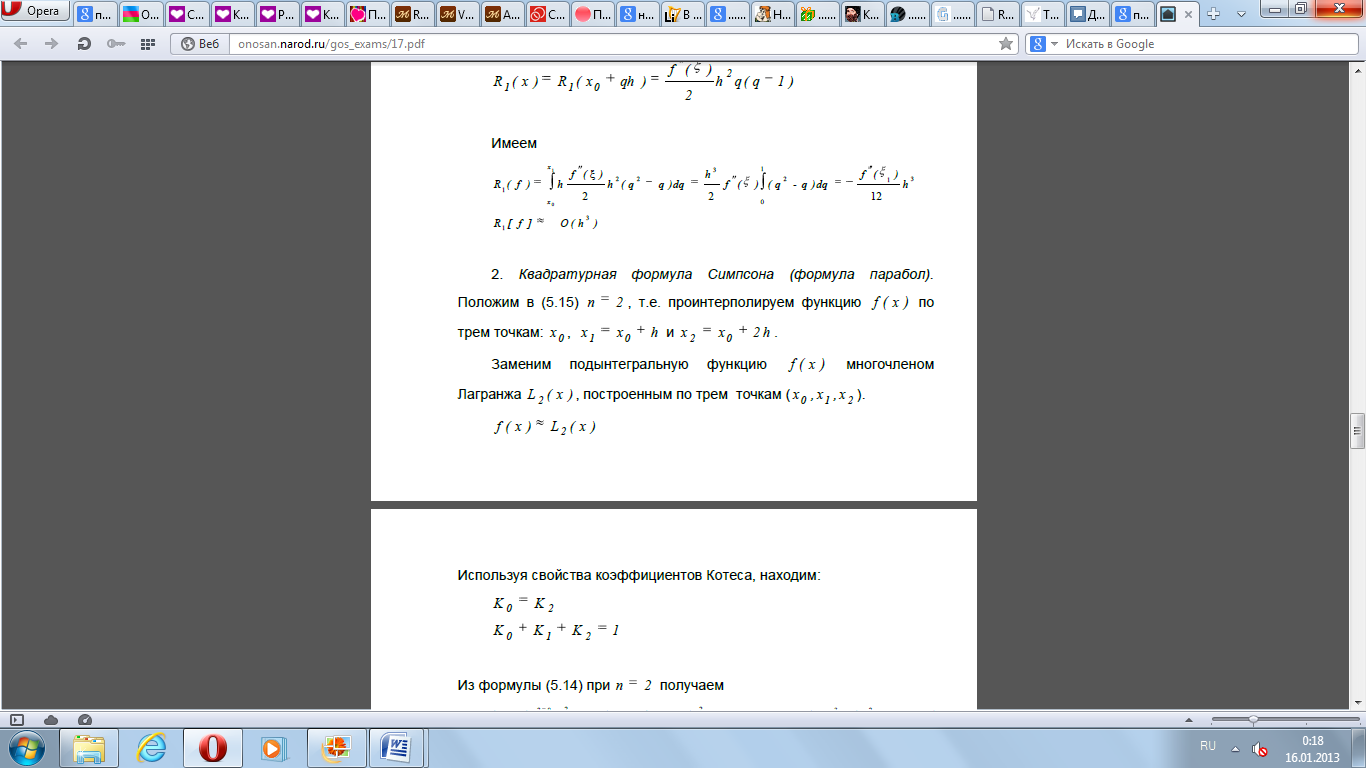
- •Составление квадратурной формулы.
- •Билет №11.
- •1. Условия сходимости итерационного процесса.
- •2. Погрешность степени и корня.
- •Билет №12.
- •1. Точные и приближенные цифры.
- •2. Интерполяционный многочлен Ньютона.
- •Билет №13.
- •1. Простейшие квадратурные формулы.
- •2. Интерполяция многочленами.
Билет №11.
1. Условия сходимости итерационного процесса.
Пусть дана система: .
Условие сходимости состоит в следующем:
Если сумма модулей элементов (строк)столбцов <1, то процесс итерации для данной системы сходится к единственному решению независимо от выбора нач.вектора:
или
Сходимость итера.процесса связана с нормальной матрицой
∣∣ ∣∣1=
||
||
2. Погрешность степени и корня.
Погрешность степени
Предельная относительная погрешность m-ой степени в m раз больше предельной относительной погрешности подкоренного числа.
δu=m•δx
Погрешность корня
Предельная относительная погрешность корня m-ой степени в m раз меньше предельной относительной погрешности подкоренного числа.
δu=(1/m)•δx
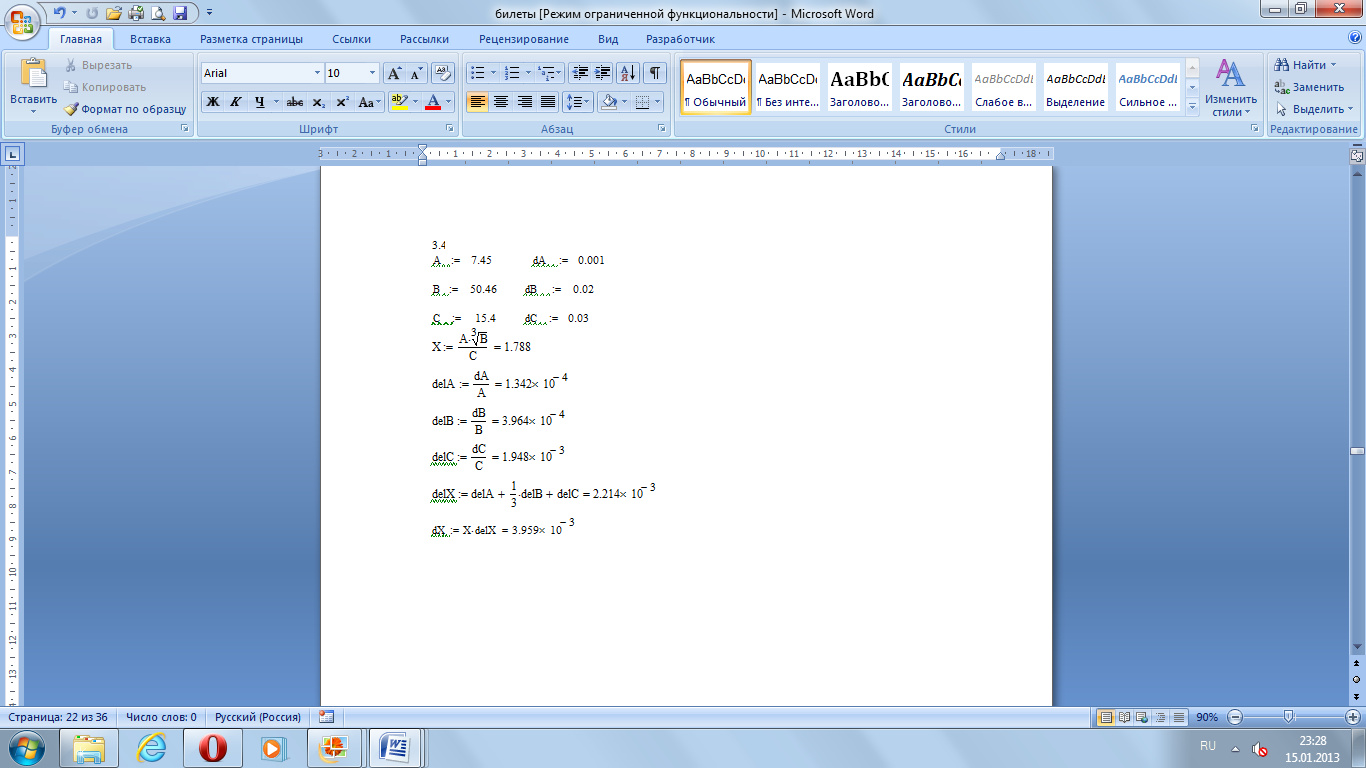
3.

4.
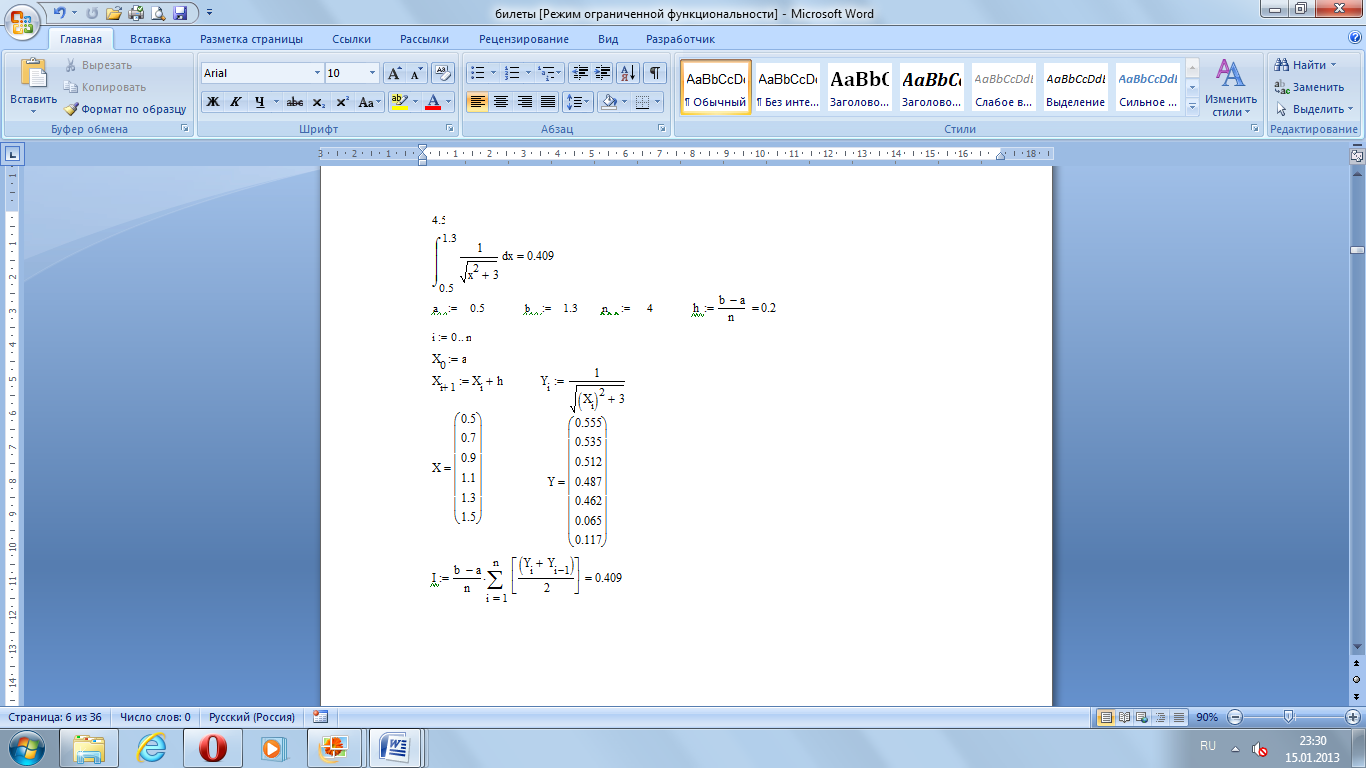
5.
Билет №12.
1. Точные и приближенные цифры.
Цифры, составляющие приближенное число, могут быть значащими, верными и сомнительными.
Верной (точной) цифрой называется цифра, погрешность которой не превышает половины единицы следующего разряда, т.е. если ∆*(а*)≤0,5∙10m-1+n (где m – число разрядов а*, n – число верных цифр в нем).
Пример
Число 3,142 является приближенным значением числа π с четырьмя точными (верными) значащими цифрами, т.к.:
│π – 3,142│ = │3,14159… - 3,142│< 0,0005 = 0,5∙103
2. Интерполяционный многочлен Ньютона.
Многочлен Ньютона интерполяционный – как и другие интерполяционные формулы, служит для построения многочлена n-й степени, который совпадает в (n+1) точке co значениями неизвестной искомой функции у = f(x).
Пусть в точках х0, х1, …, хn+1 значения функции у = f(x) равны соответственно у0 = f(x0), y1 = f(x1), …, yn+1 = f(xn+1).
Построим интерполяционный многочлен Ньютона с помощью метода неопределенных коэффициентов. Для этого запишем искомый многочлен в виде
Pn(x) = b0 + b1(x – x0) + b2(x – x0)(x – x1) + b3(x – x0)(x – x1)(x – x2) + … + bn(x – x0)…(x – xn). (1)
Последовательно подставляя в формулу (1) вместо х данные значения х0, х1, ..., хn+1, получим для нахождения неопределенных коэффициентов b0, b1, ..., bn «треугольную» систему уравнений
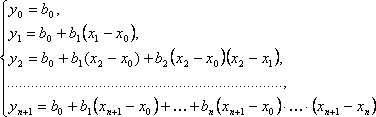
(при подстановке в равенство (1) вместо х числа х0 в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х0), обратившийся в нуль; при подстановке х = х1 обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х1) и т.д.).
Полученную систему удобно решать: из первого её уравнения находим свободный член искомого многочлена b0; подставив его во второе уравнение, находим коэффициент b1 при первой степени х в искомом многочлене:
![]()
и т.д.
Для интерполяционного многочлена Ньютона можно выписать явные выражения коэффициентов через данные задачи, а также и оценки точности замены неизвестной функции f(x) этим многочленом.
3.


4.

5.

Билет №13.
1. Простейшие квадратурные формулы.