1. Метод правых прямоугольников

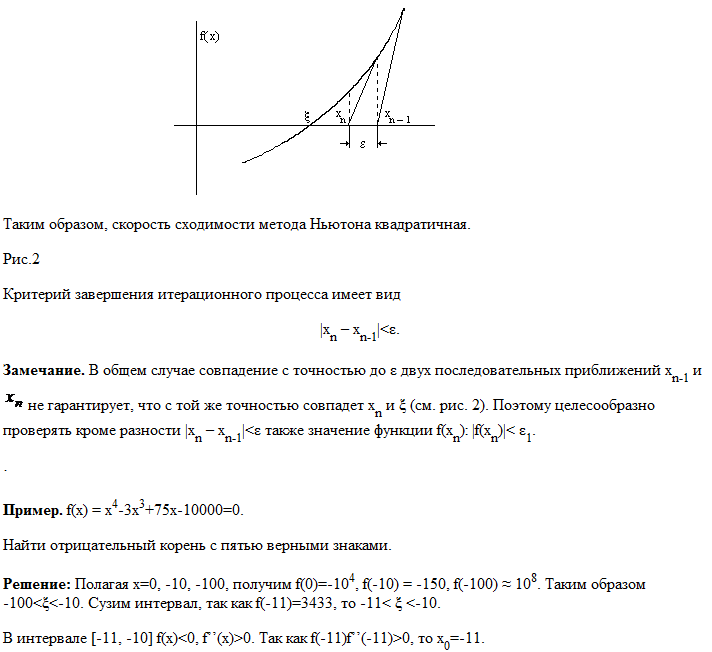
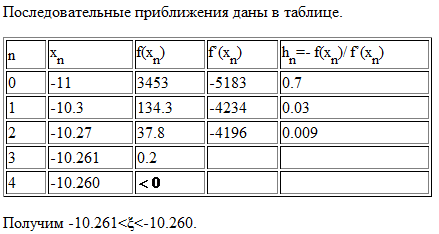
2. Метод касательных

Метод правых прямоугольников  Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка  . Точки деления будут: x₀=a; x₁=a+h; x₂=a+2× h, ... , x_n-1=a+(n-1)× h; x_n=b. Эти числа будем называть узлами. Вычислим значения функции f(x) в узлах, обозначим их y₀, y₁, y₂, ... , y_n. Cтало быть, y₀=f(a), y₁=f(x₁), y₂=f(x₂), ... , y_n=f(b). Числа y₀, y₁, y₂, ... , y_n являются ординатами точек графика функции, соответствующих абсциссам x₀, x₁, x₂, ... , x_n. Площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

Формула правых прямоугольников:

Метод касательных.

ОТСЮДА СЛЕДУЕТ

Подставим 3.16 в 3.15 и получим

Билет №7.

1. Условия сходимости итерационного процесса

2. Постановка задачи численного интегрирования

Условия сходимости итерационного процесса.

Пусть дана система: .

Условие сходимости состоит в следующем:

Если сумма модулей элементов (строк)столбцов <1, то процесс итерации для данной системы сходится к единственному решению независимо от выбора нач.вектора:

или

Сходимость итера.процесса связана с нормальной матрицой

∣∣ ∣∣1=

||

||

Постановка задачи численного интегрирования

Теперь попробуем вычислить каким-либо методом математического анализа аналогичный интеграл вида и убедимся в том, что он аналитически не вычисляется. Однако практические задачи в своем большинстве приводят именно к такого типа интегралам. Как решается эта проблема? В этих случаях применяется численное интегрирование. Кроме того, если функция y=f(x) задана таблично, то приближенное вычисление интеграла также выполняется численно.

Прежде чем переходить к численным методам подсчета интегралов, вспомним, как вводится интеграл Римана в курсе математического анализа. Проводится разбиение отрезка [a, b] на N частичных отрезков [xi-1, xi], i = 1, ..., N, внутри каждого из которых выбирается произвольная точка ξi. Далее составляется интегральная сумма:

SN=∑Ni=1 f(ξi ) (xi - xi-1 )

Тогда интеграл Римана определяется как следующий предел интегральных сумм:

Если зафиксировать число N и не переходить к пределу, то получим некоторое приближенное значение интеграла. Простейшие численные методы нахождения значения интеграла основаны на подобных соображениях.

Задача численного интегрирования состоит в нахождении приближенного значения интеграла: (4.15)

где y=f(x) - заданная функция.

Введем на отрезке [a,b] сетку :

Точки xi называют узлами сетки (i=1, ..., N), отрезки [xi-1,xi] - частичными отрезками, числа hi=xi-xi-1 называют шагами сетки (i=1, ..., N).

В качестве приближенного значения интеграла L[f] рассмотрим следующее: L_N[f] ≡ (4.16)

где li[f] - формула для приближенного вычисления интеграла на частичном отрезке [xi-1,xi].

Билет № 8