Вопрос 10
(Рациональные дроби)
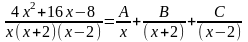
X=0 -8=A*2*(-2) x=2 16+32-8=c*2*4 x=-2
-8=-4A 40=C*8 16-32-8
A=2 C=5 -24=B4
B=-6
Вопрос 11
Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Самосопряженная (эрмитова) матрица:
Вопрос 12
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные.
В обозначении коэффициентов aij первый индекс i
обозначает номер уравнения, а второй j – номер неизвестного,
при котором стоит этот коэффициент.
Наша задача будет заключаться в нахождении решений системы.
При этом могут возникнуть три ситуации:
1)Система может иметь единственное решение.
2)Система может иметь бесконечное множество решений.
Например,
. Решением этой системы является любая
пара чисел, отличающихся знаком.
3)И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Допустимые преобразования матрицы:
1)Перестановка строк/столбцов
2) Умножение строки или столбца на число не равное 0
3) Прибавление к какой либо строке(столбцу) другой, умноженной на какое либо число.
Метод Гаусса решения систем линейных уравнений)
то метод последовательного исключения переменных,
когда с помощью элементарных преобразований система уравнений
приводится к равносильной системе ступенчатого (или треугольного) вида,
из которого последовательно, начиная с последних (по номеру) переменных,
находятся все остальные переменные
Вопрос 13
Определитель матрицы является многочленом от элементов квадратной матрицы.
Численная характеристика квадратной матрицы называется ее определителем.
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
Для матрицы 2 на 2 детерминант определяется как:
Для матрицы определитель задаётся рекурсивно:
где
— дополнительный минор к элементу
a1j. Эта формула называется разложением
по строке.
В частности, формула вычисления определителя матрицы 3 на 3 такова:
Вопрос 14
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Система из n уравнений с n неизвестными в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
Формулы крамера:
Формулы Крамера для решения систем линейных алгебраических уравнений:
1). Найти определитель матрицы
2).
3).
4).
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
AA^{-1} = A^{-1}A = E