2) Теоремы Муавра-Лапласа(без док-ва)

Локальная теорема Муавра-Лапласа Если в схеме Бернулли npq→∞, то для любого С>0 равномерно по всем │х│<=C вида x= , где m-целые неотрицательные числа, P{ }= (1+o(1)).

Интегральная теорема Муавра-Лапласа Пусть в схеме Бернулли npq . Тогда для любых -∞<A<B<∞ справедливо равенство

P{A }

Центральная предельная теорема. Если случайные величины Х1,Х2,…Хт независимы, одинаково распределены и имеют конечные математические ожидания МХ =α и дисперсии DX ,то P{ } =Ф(х).

Ошибки измерения При измерении некоторой величины α мы получаем приближенное значение Х. Сделанная ошибка δ=Х-α может быть представлена в виде суммы двух ошибок δ=(Х-МХ)+(МХ- α). Хорошие методы измерения не должны иметь систематической ошибки: МХ= α. Случайная ошибка имеет нулевое математическое ожидание Мδ=0. Пусть Dδ=σ .Для уменьшения ошибки проводится n независимых испытаний, и за оценку α берут среднее арифметическое этих измерений

= . Вычислим , какая при этом допускается погрешность. По центральной предельной теореме

P{| - α | }=P{| | } 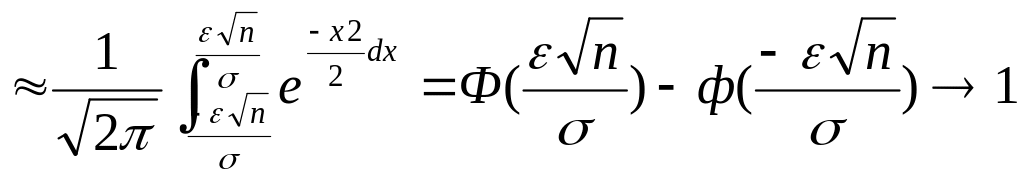при n→∞.

№18. Простейший поток событий Рассмотрим событие, наступившее в случайный момент времени(поток событий). Пример: поступление вызовов на АТС,прибытие самолетов в аэропорт и т.д..Основные св-ва:1) стационарность-вер-ть появления К события на любом промежутке времени t зависит только от К и t и не зависит от начала потока,при этом различные промежутки временине пересекаются. Вывод:если поток событий обладает св-вом стационарности,то вер-сть появления К события за t зависит только от К и t.

2) св-во отсутствия последействия:вер-ть появления К событий на любом промежутке времени зависит от того, что появилось или нет событие в в предш. момент времени,т.е. предыстория потока не сказ. На вероятности появления события в ближайшем будущем. Вывод:если поток обладает св-вом 2), то имеет место взаимная нез-ть появл. того или иного числа событий в предш. момент времени.

3) св-во ординарности:появление двух и более событий за малый промежуток времени практически невозможно, т.е. вероятность появления более одного события пренебрежительно мала по сравнению с вероятностью появления только одного события. Вывод: если поток обладает св-вом 3),то за беск. Малый промежуток времени может появится не более 1 события. ОПРЕДЕЛЕНИЕ: Простейшим (пуассоновским) потоком событий называют поток событий,обладающий св-вами 1-3. ОПРЕДЕЛЕНИЕ: Интенсивность потока : λ наз. среднее число событий, которое появляется в единицу времени. Если постоянная интенсивность известна, то вер-ть появления К событий простейшего потока за время t определяется формулой Пуассона:

Случайный процесс Набор случ. величин Х(t) опред. на (Ω,А) называют случайной функцией. Если параметр t играет роль времени, т.е. t принадлежит R , то такую случайную функцию называют случайным процессом. Если же t принадлежит {0,+-1,+-2…}, то случайную функцию называют случайной последовательностью.

Цепи Маркова —последовательность испытаний, в любом из которых появление только одного из К несовмесн. событий А1,А2,…Ак ,причем усл. вер-ть pij(S)того,что в S-ом испытании наступит событие Аj(j=1-k) при условии,что в (S-1)-м испытании было Aj(i=1-k) не зав. от рез-тов предшеств. испытания.

ЦМ являются обобщающим понятием независимых испытаний.

№19. Постановка и решение задачи линейной регрессии. Метод наименьших квадратов.

Рассмотрим 2 случайные величины X и Y, заданные на одном и том же пространстве элементарных событий. Значениям и этих случайных величин соответствуют вероятности P и P , с которыми они принимаются.

Пусть каждой паре ( , ) соответствует вероятность p( , ) того, что . Тогда говорят, что задано совместное распределение случайных величин X и Y.

Случайные величины называются независимыми, если для любых , справедливо равенство p( , )=P P .

По определению их ковариация равна Cov(X, Y)=M((X-MX)(Y-MY)), где буквой М обозначено мат.ожидание.

Через ρ(X, Y) будем обозначать коэффициент корреляции X и Y, который определяется как ρ(X, Y)= , где DX, DY – дисперсии X и Y. Если случайные величины независимы, их ковариация равна нулю. Заметим, что обратное неверно: равенство нулю ковариации и коэффициента корреляции еще не гарантирует независимости случайных величин. Из определения и неравенства Коши-Буняковского следует, что коэффициент корреляции принимает значения между -1 и +1.

Будем говорить,что между случайными величинами X и Y имеется функциональная зависимость, если существует функция F(x) такая, что Y=F(x). Если же среднее значение одной случайной величины функционально зависит от значений, принимаемых другой, то будем говорить, что такие случайные величины связаны корреляционной зависимостью.

Выразим функционально один из двух взаимосвязанных факторов через другой (хотя бы приближенно). Простейшим из таких выражений является линейное: Y=aX+b, где a и b – некоторые константы.

Если справедливо равенство, то между X и Y имеется функциональная зависимость, даже линейная. Это бывает лишь в случаях, когда ρ(X, Y)=1 или ρ(X, Y)=-1. Если же –1< ρ(X, Y)<1, равенство может выполняться лишь приближенно, при условии, что константы a и b выбраны некоторым специальным образом.

Их выбирают такими, чтобы функция F(a,b)=M((Y–aX–b) ) достигала в точке a, b минимума. Тогда в среднем квадратичном случайная величина aX+b будет менее всего уклоняться от Y.

Применив метод наименьших квадратов, найдем для a и b следующие значения:

a= ρ(X, Y) , b=MY – ρ(X, Y) MX

тогда F(a,b)=DY(1 – ρ(X, Y) ).

1. Если ρ(X, Y)>0, то при увеличении одной из случайных величин другая также имеет тенденцию к увеличению.

2. Если ρ(X, Y) <0, то при увеличении одной из случайных величин другая также будет в среднем квадратичном возрастать.

3. Если ρ(X, Y)=0, то при любых a, b M((Y – aX – b) )≥DY. Следовательно, ни при каких a, b случайная величина aX+b не может в среднем квадратичном приблизить случайную величину Y лучше, чем константа MY(среднее значение Y).

4. Если –1< ρ(X, Y)<1, то при a,b M((Y–aX–b) )= DY(1 – ρ(X, Y) ). Следовательно, случайная величина aX+b в среднем квадратичном лучше приближает Y, чем MY, причем тем лучше, чем больше ‌‌ ‌.

5. Если ρ(X, Y)=1 или ρ(X, Y)= –1, то равенство Y=aX+b выполняется с вероятностью 1.