1.10 Игровые деревья.
Для любой игры можно определить игровое дерево, узлы которого суть игровые позиции, а дочерние узлы – позиции, достижимые из исходной за один ход.
Также полагается, что дерево конечно, т.е. мы имеем дело с игрой которая не длится вечно или имеет бесконечно много ходов из одной позиции.
рис. 1 Фрагмент игрового дерева
Многие сложные реальные задачи можно смоделировать с помощью деревьев решений (decision trees). Каждый узел в дереве представляет собой один шаг решения задачи. Ветвь в дереве соответствует решению, которое ведет к более полному решению. Листы представляют собой окончательное решение. Цель состоит в том, чтобы найти «наилучший» путь от корня до листа при выполнении некоторых условий. Естественно, что условия и «наилучший» путь зависят от сложности конкретной задачи.
На примере крестиков-ноликов показаны способы поиска в деревьях игры наилучшего возможного хода. Последующие разделы описывают более общие способы исследования деревьев решений. Для самых маленьких деревьев можно использовать метод полного перебора(exhaustive searching) всех возможных решений. Для работы с большими деревьями более подходит метод ветвей и границ(brunch-and-bound technique), позволяющий отыскивать лучшее возможное решение без поиска по всему дереву. Для огромных деревьев лучше использовать эвристический метод (heuristic). При этом найденное решение может и не быть наилучшим из возможных, но должно быть достаточно близким к нему.
1.11 Дерево игры в нарды
Возможность игрока передвигать шашки определяется броском двух кубиков. Существует 36 равновероятных комбинаций выпадения кубиков, из них 21 принципиально разная. В сети интернет можно найти большое количество материалов по нескольким различным подходам к программированию игрока в нарды. Некоторая систематизация этих материалов произведена авторами.
Игра описывается посредством дерева игры. Далее также по аналогии определяются оценки позиций, применяется а,b - эвристика. Кроме того, вводится такое новое понятие, как функция риска.
Так как нарды в большой степени отличаются от игр, подобных шахматам, то некоторые подходы не применимы в отношении нард. Основным отличием нард от шахмат является недетерминированность. Её привносит в нарды стохастический фактор, обусловленный бросанием кубиков. Этот фактор значительно усложняет исследование нард, но в то же время делает его более актуальным. Ведь подавляющее большинство явлений и процессов в действительности так или иначе связано с явлениями случайными, описываемыми вероятностно. В результате, дерево игры в нарды - дерево недетерминированной игры. В связи с этим возникает потребность дополнительном анализе дерева игры в нарды.
Учитывая то, что у нард очень большой коэффициент ветвления дерева игровых позиций (достигает 200-300 доступных ходов из одной позиции) и наличие случайности (броски костей) перебор в осложняется, вследствие ограниченности вычислительных ресурсов. Для примера, в шахматах коэффициент ветвления составляет порядка 40 ходов, а для шашек 8-15. Так например при глубине поиска два существует 1,296 ходов, глубина 3 – 46,656 ходов. Поэтому рассматриваются наиболее вероятные ходы, например выпадение дубля несколько раз подряд маловероятно. При таком подходе число учитываемых ходов сокращается до 900 и 27,000 соответственно. Но даже такой подход не позволяет осуществлять перебор ходов на большую глубину, т.к. их количество слишком велико, и время работы существенно увеличивается. В следствие этого расчет ходов более чем на глубину 2 не целесообразен. На рисунке 3. показана зависимость количества вариантов ходов от глубины.
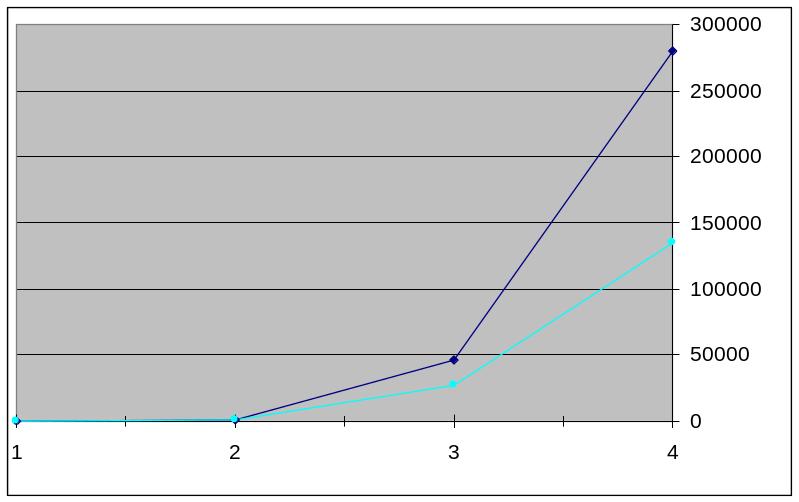
Рисунок 3. Зависимость количества вариантов ходов от глубины.
Поэтому необходима качественная оценочная функция, дающая правдоподобную оценку вероятности победы игрока в данной позиции.
Что представляет из себя просмотр дерева игры и поиск в нем ходов? При поиске ходов мы хотим создать в перспективе наиболее выгодную ситуацию, желательно через как можно большее количество ходов, нас интересует больше ситуация в будущем, а не в настоящем, поэтому и прибегают к дереву игры. Причем, скорее всего выгодной ситуации в будущем будут предшествовать не самые выгодные промежуточные ходы. Необходимо также учитывать наличие противника, который предположительно будет ходить оптимально со своей точки зрения и стараться ухудшить ситуацию для соперника.
Итак, строится дерево заданной глубины, в корне которого текущая ситуация, а листья которого (на самой большой глубине) соответствуют терминальным ситуациям, после которых улучшение невозможно. Фактически в большинстве случаев оно возможно, но эта возможность скрыта от нас ограниченностью дерева поиска.
Среди терминальных ситуаций требуется выделить лучшую с точки зрения того игрока, для которого мы ищем ход и достижимую при условии наиболее оптимального сопротивления второго игрока.
Качество хода определяется оценочной функцией, которая применяется к конкретной позиции на доске. Оценочная функция может вычисляться с точки зрения одного или другого игрока, например, количество белых или черных фишек.