Индекс рентабельности (pi)
Дисконтированный индекс доходности (ТС-индекс, PV-index, Present value index, Discounted Profitability Index, DPI)(иногда называемый отношением дохода к издержкам (benefit cost ratio), выраженным в текущих стоимостях).
Формула для расчета дисконтированного индекса доходности:
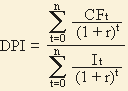
DPI >= 1,0
CFt - приток денежных средств в период t; It - сумма инвестиций (затраты) в t-ом периоде; r - барьерная ставка (ставка дисконтирования); n - суммарное число периодов (интервалов, шагов) t = 0, 1, 2, ..., n.
Задача 1.76.
Размер инвестиции - 115000$. Доходы от инвестиций в первом году: 32000$; во втором году: $41000; в третьем году: $43750; в четвертом году: $38250.Размер барьерной ставки - 9,2%.
Пересчитаем денежные потоки в вид текущих стоимостей:
PV1 = 32000 / (1 + 0,092) = $29304,03 PV3 = 43750 / (1 + 0,092)3 = $33597,75
PV2 = 41000 / (1 + 0,092)2 = $34382,59 PV4 = 38250 / (1 + 0,092)4 = $26899,29
DPI = (29304,03 + 34382,59 + 33597,75 + 26899,29) / 115000 = 1,07985
Ответ: дисконтированный индекс доходности равен 1,079
2. Облигации и процентные ставки
2.1. Определение цены облигации
Задача 2.1.
Облигации 1000 руб., купон 10%, выплачивается один раз в год. До погашения облигации 3 года. Определить цену облигации, если ее доходность до погашения должна составить 12%.
Решение.
Принцип расчета цены облигации основан на дисконтировании будущих доходов, которые будут выплачены по ней. Технику определения курсовой стоимости можно представить в три действия:
1) определяем поток доходов, который ожидается по бумаге;
2) находим дисконтированную стоимость величины каждого платежа по бумаге; дисконтирование осуществляем под процентную ставку, соответствующую доходности до погашения облигации1;
3) суммируем дисконтированные стоимости; полученная сумма и является ценой облигации.
В задаче поток доходов по облигации представлен выплатой купонов и ем номинала. По купону в конце каждого года выплачивается сумма:
1000 руб.∙0,1 = 100руб.
В конце третьего года также погашается номинальная стоимость бумаги. Таким образом,
облигация принесет следующий поток доходов:
Год |
1 |
2 |
3 |
Сумма (руб.) |
100 |
100 |
1100 |
Дисконтированные стоимости платежей для каждого года соответственно равны:
Год |
1 |
2 |
3 |
Дисконтированная стоимость (руб.) |
|
|
|
Цена облигации равна:
89,29+ 79,72+ 782,96 = 951,97руб.
Задача 2.2.
Номинал облигации 1000 руб., купон 10%, выплачивается один раз в год. До погашения облигации 3 года. Определить цену облигации, если ее доходность до погашения должна составить 8%.
Решение.
В соответствии с алгоритмом определения стоимости облигации, представленном в задаче 2.1, формула расчета цены облигации имеет вид:
(2.1)
где Р — цена облигации; С — купон в рублях; N — номинал;
n — число лет до погашения облигации;
r — доходность до погашения облигации.
Согласно формуле (2.1) цена облигации равна:
Задача 2.9.
Номинал облигации 1000 руб., купон 10%, выплачивается два раза в год. До погашения облигации 2 года. Определить цену облигации, если ее доходность до погашения должна составить 8%.
Решение.
Когда купон выплачивается m раз в год, формула (2.1) принимает вид:
(2.2)
Согласно (2.2) цена облигации равна:
Примечание.
Данную задачу можно решить, используя формулу (2,1), только в этом случае периоды времени выплаты купонов следует учитывать не в купонных периодах, а, как и раньше, в годах. Первый купон выплачивается через полгода, поэтому для него время выплаты равно 0,5 года, второй купон выплачивается через год, для него время выплаты равно 1 год и т.д. Ставка дисконтирования учитывается в этом случае как эффективный процент на основе заданной доходности до погашения, т.е. она равна:
(1+0,08/2)2 - 1= 0,0816.
Согласно формуле (2.1) цена облигации составляет:
руб.