4.3. Риск портфеля ценных бумаг

Задача 4.43.

Доходность двух активов за 8 периодов представлена в таблице:

Периоды	1	2	3	4	5	6	7	8
Доходность актива X	10	14	10	8	-5	-3	3	7
Доходность актива Y	14	18	13	10	-2	-7	-2	10

Определить коэффициент выборочной ковариации доходностей активов.

Решение.

Коэффициент выборочной ковариации определяется по формуле:

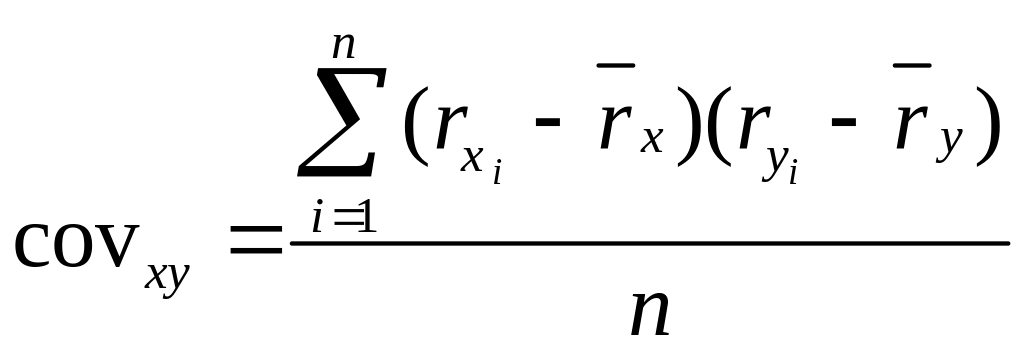(4.9)

где: r_xi, r_yi -доходности активов Х и Y в i-м периоде;

-средняя доходность актива X;

- средняя доходность актива Y;

п - число периодов наблюдения.

Определяем среднюю доходность активов:

Ковариация доходностей равна:

Задача 4.44.

На основе данных задачи 4.43 определить коэффициент корреляции доход­ностей

активов X и Y.

Решение.

Коэффициент корреляции определяется по формуле:

(4.10)

где: corr_xv — коэффициент корреляции переменных X и Y;

- стандартное отклонение переменой X;

- стандартное отклонение переменой Y.

Определяем дисперсии доходностей активов согласно формуле (4.1):

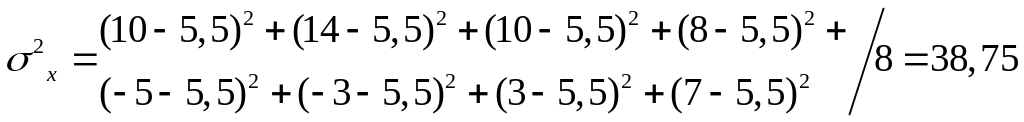
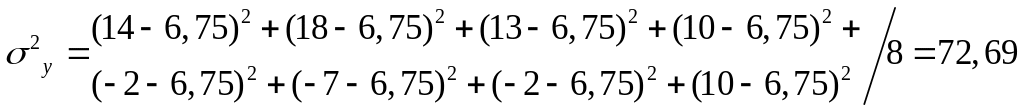
Стандартные отклонения доходностей равны:

Коэффициент корреляции составляет:

.

5. Модели оценки стоимости активов

5.1 Модель оценки стоимости активов (сарм)

Задача 5.1.

Ставка без риска равна 10%, ожидаемая доходность рыночного портфеля – 20%, стандартное отклонение доходности рыночного портфеля - 15% . Определить ожидаемую доходность портфеля, стандартное отклонение доходности которого составляет 30%.

Решение.

Ожидаемая доходность портфеля определяется с помощью уравнения CML:

(5.1)

где: - риск i-го портфеля, для которого определяется уровень ожидаемой доходности;

- ожидаемая доходность i-го портфеля;

- риск рыночного портфеля;

- ожидаемая доходность рыночного портфеля.

Согласно уравнению (5.1) ожидаемая доходность портфеля равна:

Задача 5.2.

Ставка без риска равна 8%, ожидаемая доходность рыночного портфеля – 22%, стандартное отклонение доходности рыночного портфеля — 14%. Определить ожидаемую доходность портфеля, стандартное отклонение доходности которого составляет 25% .

Решение.