Глава 4. Доходность и риск портфеля ценных бумаг
4.1. Ожидаемая доходность актива
И портфеля ценных бумаг
Задача 4.1.
Данные о доходности актива за прошедшие 10 лет представлены в таблице:
Годы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Доходность (%) |
10 |
14 |
10 |
8 |
-5 |
-3 |
3 |
7 |
16 |
Определить ожидаемую доходность актива.
Решение.
На
основе прошлых данных статистики
ожидаемая доходность актива определяется
как среднеарифметическая доходность
(
):
Задача 4.2.
Данные о доходности актива за прошедшие 9 лет представлены в таблице:
Годы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Доходность (%) |
6 |
4 |
-1 |
2 |
5 |
8 |
3 |
4 |
10 |
Определить ожидаемую доходность актива.
Ответ.
=4,56%.
Задача 4.3.
Данные о доходности актива за прошедшие 9 месяцев представлены в таблице:
Годы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Доходность (%) |
3 |
-2 |
-1 |
2 |
6 |
5 |
8 |
10 |
12 |
Определить ожидаемую доходность в расчете на месяц.
Ответ.
=
4,78%.
Задача 4.4.
Инвестор полагает, что в будущем году можно ожидать следующего вероятностного распределения доходности актива.
Доходность (%) |
Вероятность (%) |
-10 |
3 |
-5 |
7 |
0 |
12 |
5 |
15 |
10 |
17 |
15 |
20 |
20 |
16 |
25 |
7 |
30 |
3 |
Определить ожидаемую доходность актива.
Решение.
Ожидаемая доходность актива определяется как среднеарифметическая взвешенная доходность. Весами выступают вероятности каждого возможного исхода.
.
4.2. Риск актива
Задача 4.17.
Доходность актива за 8 лет представлена в таблице:
-
Годы
1
2
3
4
5
6
7
8
Доходность
(%)
10
14
18
16
-10
-5
6
15
Определить риск актива, представленный показателями выборочной дисперсии и стандартного отклонения доходности.
Решение.
Выборочная дисперсия доходности актива определяется по формуле:
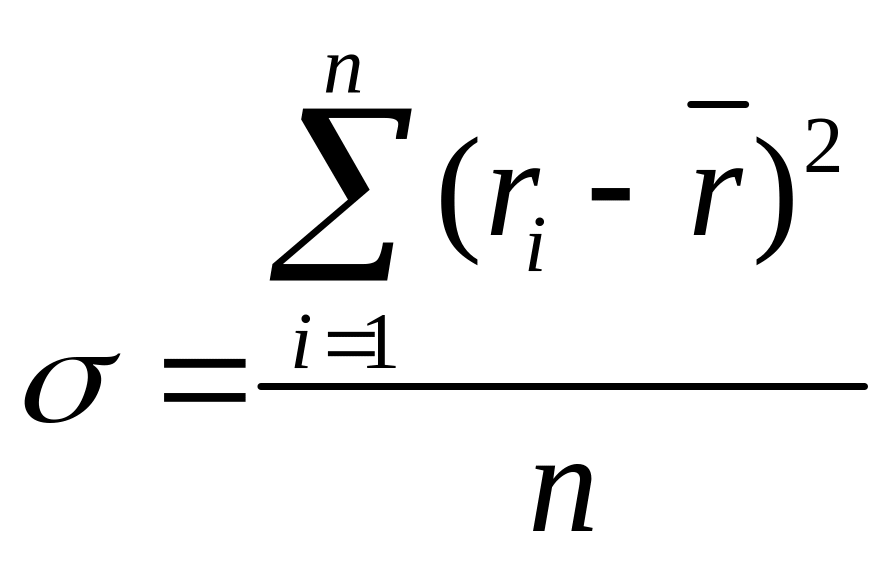(4.1)
где: r1 — доходность актива в i- м периоде;
_
r — средняя доходность актива;
n - число периодов наблюдения.
Средняя доходность определяется по формуле:
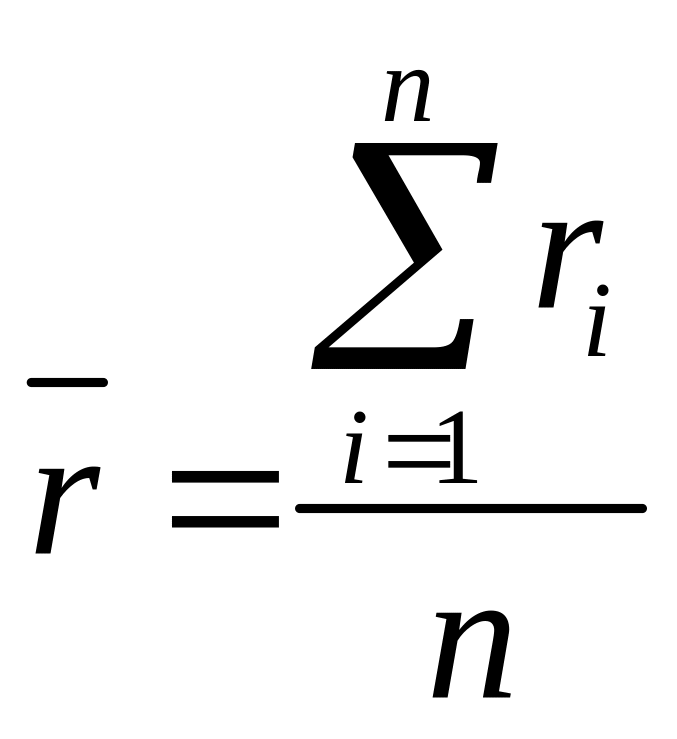
Средняя доходность актива за 8 лет составила:
Выборочная дисперсия доходности актива равна:
σ 2 =(10-8)2 +(14-8)2 +(18-8)2 +(16-8)2 +(-10-8)2 +(-5-8)2 +(б-8)2+(15-8)2/8 = 93,75.
Стандартное отклонение доходности определяется как корень квадратный из дисперсии:
Выборочное стандартное отклонение доходности равно:
=
9,68%
Задача 4.18.
На основе данных задачи 4.17 определить, какую доходность инвестор может получить по активу через год с вероятностью
а) 68,3%,
б) 95,4%,
в) 99,7%?
Распределение доходности актива предполагается нормальным.
Решение.
Как было определено в задаче 4.17, ожидаемая доходность актива равна 8%, стандартное отклонение 9,68%.
а) С вероятностью 68,3% можно ожидать, что доходность актива через год будет располагаться в интервале одного стандартного отклонения от ожидаемой доходности, т.е. 8 ±9,68 или:
от 8-9,68 = -1,68% до 8 + 9,68 = 17,68%.
б) С вероятностью 95,4% можно ожидать, что доходность актива через год будет располагаться в интервале двух стандартных отклонений от ожидаемой доходности, т.е. 8 ± 2∙ 9,68 или:
от 8-2∙9,68 = -11,36% до 8 + 2∙9,68 = 27,36%.
в) С вероятностью 99,7% можно ожидать, что доходность актива через год будет располагаться в интервале трех стандартных отклонений от ожидаемой доходности, т.е. 8 + 3∙9,68 или:
от 8-3∙9,68 = -21,04% до 8 + 3∙9,68 = 37,04%.
Задача 4.19.
На основе данных задачи 4.17 определить исправленную дисперсию и
стандартное отклонение доходности актива.
Решение.
Исправленная дисперсия доходности актива определяется по формуле:
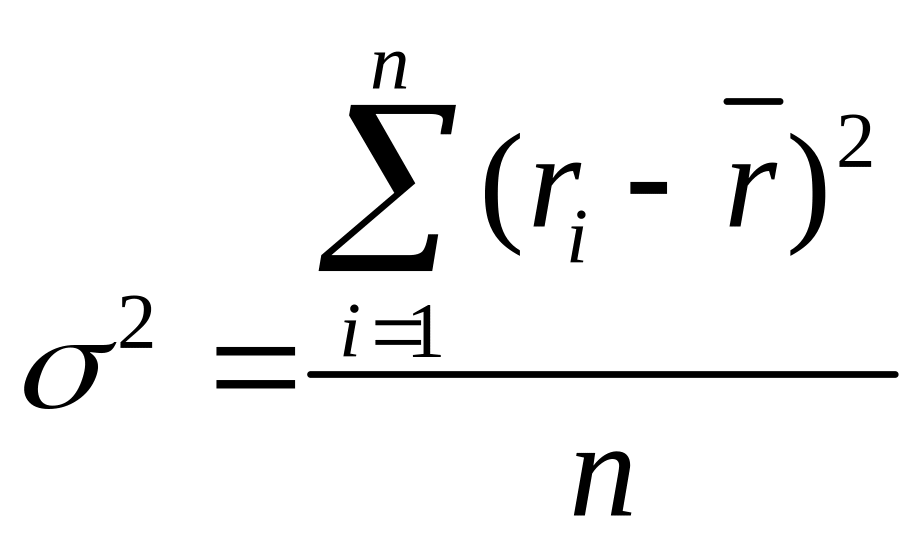(4.2)
Исправленная дисперсия доходности актива равна:
σ 2=(10-8)2+(14-8)2 + (18-8)2+(16-8)2+(-10-8)2 +
+(-5-8)2 + (б-8)2+(15-8)2/(8-1) = 107,14.
Исправленное стандартное отклонение доходности составляет:
=10,35.
Задача 4.20.
Доходность актива за 10 дней представлена в таблице:
-
Дни
1
2
3
4
5
6
7
8
9
10
Доходность
(%)
0,1
0,5
1,2
-0,4
-0,2
-0,01
0,3
0,6
-0,05
1,3
Определить риск актива, представленный показателями выборочной
дисперсии и стандартного отклонения доходности.
Решение.
Средняя доходность актива в расчете на день равна:
Выборочная дисперсия доходности актива в расчете на один день согласно формуле (4.1) составляет:
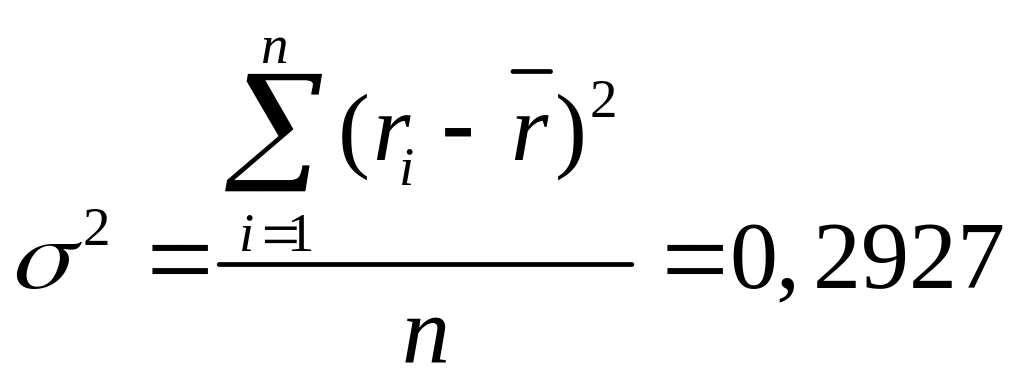
Стандартное отклонение доходности за один день равно:
=
0,541%.