1. Арифметика финансового рынка Оценка эффективности инвестиций

Необходимо отметить, что при инвестировании всегда существует определенный интервал времени — так называемый инвестиционный (холдинговый) период — между моментом вложения инвестиций и получением прибыли (иного положительного эффекта). Поэтому в самом общем смысле под инвестированием понимают процесс вложения инвестиций сегодня ради получения прибыли по окончании холдингового периода. Иными словами, принимая решение о вложении инвестиций, инвестор фактически отказывается от текущего потребления инвестируемых средств, чтобы в конце холдингового (инвестиционного) периода получить определенный положительный эффект.

Длительность холдингового периода определяет условное различие между игрой, спекуляцией и инвестированием. Под игрой понимают инвестирование с очень коротким холдинговым периодом (порой несколько секунд — сколько необходимо, например, для вращения рулетки). Существуют и другие отличия игры. Так, рациональный инвестор рассматривает игру как развлечение, а не как способ получения дохода. Риск игры является искусственно созданным, а не объективно возникшим в процессе функционирования рынка; этот риск не обеспечивает разумного сочетания с ожидаемой отдачей, вследствие чего для игрока ожидаемая величина отдачи отрицательна, что алогично с точки зрения инвестирования. Спекуляция длится дольше игры, но ее холдинговый период все же не превосходит нескольких недель. Именно такой период имеет в виду спекулянт (который также является инвестором), приобретая какое-либо средство в надежде на скорое повышение его цены. Строго говоря, нет теоретически обоснованного определения холдингового периода инвестирования, которое бы четко отделяло его от игры и спекуляции. Как правило, большинство западных специалистов сходятся во мнении, что холдинговый период инвестирования должен превышать 6 месяцев.

Отдача и доходность инвестиций

Под отдачей инвестиций обычно понимают прирост денежных средств инзестора вследствие проведения инвестиционной деятельности. Так, если инвестор инвестировал 100 тыс. руб. и по прошествии холдингового периода получил 108 тыс. руб., то можно сказать, что отдача инвестиций (т. е. увеличение денежных средств) в этом случае составляет 8 тыс. руб.

Суммы, направляемые инвестором в различные инвестиционные объекты, и отдача этих вложений отличаются друг от друга. Зачастую поэтому сравнение абсолютных величин инвестиционных затрат и отдачи инвестиций не дает четкого представления о степени выгодности инвестиций. Действительно, пусть инвестор имеет возможность вложить средства в два инвестиционных объекта: один стоимостью 150 тыс. руб. и другой 180 тыс. руб.; при этом отдача первого объекта составляет 15 тыс. руб., а второго — 16 тыс. руб. Какое вложение предпочтительней? Казалось бы, что второй объект дает более высокую отдачу (16 тыс. по сравнению с 15 тыс. руб.), но житейский опыт подсказывает, что 16 тыс. руб., полученных на 180 тыс. руб. инвестиционных затрат, менее выгодны, чем 15 тыс. руб., но на 150 тыс. руб. первоначальных затрат.

В этой связи для принятия инвестиционного решения целесообразно оперировать не абсолютными, а относительными величинами и ввести понятие доходности (нормы отдачи) инвестиций:

(1.1)

Доходность можно задать двумя способами — либо как относительную ве­личину, либо в виде процента. Например, в рассматриваемом примере в первом случае доходность:

r =(165-150)/150 = 0,1,

а во втором случае:

r = (196 - 180)/180 = 0,089.

Чтобы задать доходность в виде процента, необходимо полученные относительные величины умножить на 100%. В первом случае доходность равна:

r = 0,1*100% = 10%

а во втором случае:

r =0,089*100% = 8,9%.

Отсюда очевидно, что первый вид инвестирования более предпочтительный.

Когда рассматриваются инвестиции в ценные бумаги, то следует иметь в виду, что ряд ценных бумаг обеспечивает увеличение денежных средств не только вследствие повышения их стоимости в ходе холдингового периода, но и путем периодической выплаты дополнительных денежных сумм (например, дивиденда по акции, процентных выплат по облигации). В этой связи можно указать другие формулы вычисления доходности инвестиций r:

,

.

например, пусть инвестор купил акцию за 10 руб. В конце года ее цена возросла до 11 руб., а годовой дивиденд составил 0,5 руб. Тогда доходность этой акции составит:

Г=(11-10 + 0,5)/10 = 0,15,или15%.

Пусть инвестор намерен приобрести ценную бумагу начальной стоимостью Р_{начальн} и намерен держать ее в течение установленного им холдингового периода. По его оценкам, в конце холдингового периода цена этой ценной бумаги составит Р_конечн и за холдинговый период она обеспечит дополнительный доход D. В таком случае инвестор в состоянии оценить желаемую, требуемую для него доходность этой ценной бумаги:

.(1.2)

Если такая доходность не будет обеспечиваться данной ценной бумагой, то инвестор предпочтет альтернативный способ инвестирования.

Обратим внимание на важную деталь: как видно из формулы (1.2), снижение величины Р_{начальн} ведет к повышению требуемой доходности. Поскольку сумма Р_{начальн} представляет собой цену финансовых инструментов в исходный, текущий момент времени, а Р_конечн — ожидаемую цену в конце холдингового периода, то отсюда вытекает фундаментальное свойство рынка ценных бумаг: снижение рыночной цены обращающихся на рынке ценных бумаг приводит к росту их требуемой доходности.

Если инвестор вложил в инвестиционный объект сумму S_{начальн} и доходность этой инвестиции составляет r %, то по окончании холдингового периода он получит сумму:

S_конечн=(l+r)*S_{начальн}

Составляющие требуемой доходности инвестиций

Когда инвестор делает выбор и отказывается от текущего потребления ради адекватного дохода в будущем, то он желает получить в конце холдингового периода требуемую доходность. Многолетние наблюдения, проведенные в странах с развитыми рынками, показывают две важные особенности требуемой доходности: во-первых, общий уровень требуемой доходности для всех типов инвестиций подвержен значительным колебаниям во времени, во-вторых, существует большое различие между требуемыми доходностями альтернативных инвестиционных объектов. В этой связи важно раскрыть составляющие требуемой доходности и попытаться выявить причины отмеченных особенностей.

В общем случае на требуемую доходность оказывают воздействие три фактора:

• временной;

• фактор инфляции;

• фактор риска.

Воздействие временного фактора свидетельствует о том, что когда инвестор вкладывает средства в инвестиционный объект, то он отказывается от возможности потратить свои средства на потребление в текущий момент ради получения более высокого дохода в будущем. Иными словами, отдача инвестиционного объекта должна компенсировать инвестору откладывание текущего потребления вне зависимости от воздействия инфляции и риска, т.е. компенсировать воздействие только фактора времени.

Влияние временного фактора позволяет оценить безрисковая реальная ставка процента R_{f, реальн} (реальными называются величины, свободные от инфляционной составляющей и измеренные в базовых величинах). В противоположность реальным величинам номинальные величины содержат внутри себя инфляционную составляющую. Следует учитывать, что наблюдаемые на рынке текущие значения процентных ставок и цен всегда являются номинальными. Тот факт, что R_{f, реальн} является безрисковой, означает отсутствие какой-либо неопределенности по поводу соотношения текущего и будущего потребления, т. е. инвестор точно знает, какую отдачу принесет ему инвестиционный объект. Зачастую эту ставку процента называют чистой ставкой процента; считается, что она отражает временную стоимость денег.

Два фактора влияют на величину R_{f, реальн} — субъективный и объективный. Субъективный фактор предполагает оценку самим инвестором стоимости откладывания его текущего потребления ради будущего дохода, что определяет требуемое инвестором вознаграждение, ставку компенсации за задержку в потреблении. Эта ставка различна для каждого инвестора, однако под воздействием спроса и предложения на рынке ссудного капитала устанавливается ее равновесная величина.

Объективный фактор — это инвестиционные возможности экономики страны в текущий момент. Они зависят от долговременного реального уровня развития экономики: изменения в темпах развития экономики воздействуют на все инвестиционные проекты и влекут перемены в требуемой доходности всех инвестиций. Реальный уровень развития экономики связан с долговременными темпами прироста рабочей силы и ростом производительности труда. Существует положительная связь между инвестиционными возможностями экономики и безрисковой ставкой процента — повышение темпов роста экономики вызовет и увеличение R_{f, реальн} .

Итак, первая составляющая доходности — реальная безрисковая ставка процента — компенсирует инвестору откладывание текущего потребления (временной фактор).

Оценка фактора инфляции. Приведенная выше безрисковая ставка определена при условии неизменности общего уровня цен (отсутствия инфляции) за холдинговый период, т. е. является реальной ставкой. Между тем, если инвестор ожидает рост общего уровня цен, то требуемая им номинальная безрисковая ставка должна компенсировать и будущие потери из-за инфляции. Значит, вторая составляющая требуемой доходности учитывает фактор инфляции.

Представим, что суммарное воздействие субъективных оценок всех инвесторов и объективного фактора обусловило величину реальной безрисковой ставки R_{f, реальн}, а планируемый уровень инфляции за холдинговый период составляет i%. Если начальная величина инвестиций S_н , то по прошествии холдингового периода инвестиционный объект должен обеспечить сумму S_k, равную:

S_k =S_н*(1+R_реальн)*(1+i),

что и определяет требуемую компенсацию инвестору с учетом инфляции, т.е.:

S_k =S_н*(1+R_{f, реальн})*(1+i)=Sн*(1+R_{f, реальн}).

Отсюда можно найти выражения, как для реальной, так и номинальной безрисковой ставки:

Итак, вторая составляющая доходности компенсирует инвестору ожидаемый рост общего уровня цен (фактор инфляции).

Оценка фактора риска. Вкладывая деньги в тот или иной инвестиционный объект, инвестор может лишь с определенной долей уверенности прогнозировать его будущую отдачу. Инвестор понимает, что ожидаемая им отдача может существенно отличаться от фактической отдачи, которая будет наблюдаться пo прошествии холдингового периода — он приобретал акции в надежде на быстрый рост их цены, а на самом деле цена акций понизилась. Отсутствие у инвестора 100%-ной гарантии получения планируемого дохода от инвестиций и составляет основу риска инвестирования. Значит, в общем случае требуемая доходность является случайной величиной и для ее исследования необходимо использовать аппарат теории вероятности и математической статистики.

Если инвесторы считают, что риск инвестирования в ценную бумагу им компенсирует надбавка за риск R _риск, то тогда искомая номинальная рисковая она же и текущая рыночная) величина доходности ценной бумаги R _{риск, номинальн} будет равна:

R_{риск, номинальн}=R _{f, номинальн}+R_риск .

Следует иметь в виду, что любая требуемая доходность (процентная ставка, доходность конкретной ценной бумаги) содержит упомянутые три составляющие.

На основании изложенного можно следующим образом определить понятие инвестирования: инвестирование — процесс вложения инвестиций в определенный момент времени в тот или иной инвестиционный объект с целью получения в будущем потока доходов, компенсирующих инвестору:

а) откладывание текущего потребления (временной фактор);

б) ожидаемый рост общего уровня цен (фактор инфляции);

в) неопределенность получения будущего потока денег (фактор инвестиционного риска).

Оценка риска инвестиций

Как отмечалось, вкладывая деньги в тот или иной инвестиционный объект, инвестор может лишь с определенной долей уверенности прогнозировать будущую отдачу инвестиций.

Для количественного описания степени объективной возможности наступления того или иного случайного события r вводится специальная числовая функция Р(r), называемая вероятностью события r. В применении к доходности r можно считать, что вероятность показывает относительную частоту появления того или иного значения r.

Предположим, что мы сделали 100 наблюдений доходности определенной инвестиции и получили результаты, приведенные в табл. 1.3.

Вероятность в данном случае показывает относительную частоту появления ожидаемой величины: вероятность доходности r, находится как отношение числа наблюдаемых подобных результатов к общему числу наблюдаемых событий: P₁=15/100=0,15.

Таблица 1.3

Данные для расчета вероятности

Доходность	Количество наблюдаемых результатов	Вероятность
r1=5%	15	P1=0,15
r2=7%	20	P2=0,20
r3=10%	25	P3=0,25
r4=12%	30	P4=0,30
r5=15%	10	P5=0,10

Для вероятностей применимы пять основных правил:

1. Вероятность никогда не бывает отрицательной величиной.

2. Вероятность не может быть больше 1 (или 100%).

3. Сумма вероятностей всех возможных результатов наблюдений равняется 1.

4. Если результат события вполне предопределен, то вероятность этого события равна 1; никакой другой результат невозможен.

5. Если событие не может произойти, то считается, что его вероятность равна нулю.

В силу неопределенности доходности инвестиций инвестор должен оценивать среднюю, или ожидаемую, доходность. Ожидаемая доходность Е(r) — это взвешенная средняя величина всех возможных значений доходности, где вес каждой доходности определяется вероятностью ее появления. Иными словами, если было проведено п измерений величины r и вероятность доходности r_t равна Р_t ,то:

. (1.3)

Вычислим ожидаемое значение доходности в рассматриваемом примере:

= 0,15*0,05+0,20*0,07+0,25*0,10 + 0,30*0,12+0,10*0,15 = 0,0975 или 9,75%.

В математической статистике количественно степень риска инвестиций оценивают с помощью специальной величины — дисперсии σ², которая представляет собой средневзвешенное значение квадратов отклонений наблюдаемых величин доходности r_t от средней (ожидаемой) величины Е(r) :

Дисперсия . (1.4)

Для нашего примера:

= 0,15*[0,05-0,0975]^2+0,2*[0,07-0,975]^2 + ... + 0,1*[0,15-0,975]^2=0,00643.

Чем выше дисперсия, тем больше разброс вероятных событий и тем выше риск инвестиций.

Чаще для количественного измерения риска используют величину стандартного (среднеквадратичного) отклонения σ. По определению σ равняется квадратному корню из величины дисперсии:

. (1.5)

Среднеквадратичное отклонение σ имеет размерность случайной величины доходности r (процент) и определяет некоторый стандартный среднеквадратичный интервал рассеивания случайных величин r_t, симметричный относительно ожидаемого (среднего) значения доходности Е(r). Для нашего примера:

Как и в случае дисперсии, можно утверждать, что чем выше среднеквадратичное отклонение случайных величин доходности, тем более рискованными являются инвестиции.

В дальнейшем мы будем оперировать случайными величинами доходности, полагая, что эти случайные величины распределены по нормальному (гауссовскому) закону. В случае нормального распределения доходности r вероятность попадания случайной величины r в интервал [r₁,r₂] можно найти по формуле:

(1.6)

где Ф(r) - функция распределения случайной величины. Она определяет вероятность того, что случайная величина R примет значение, которое меньше фиксированного действительного числа г, т. е. Ф(r) = P(R<r) . Значения функции Ф(r) находят по таблице (см. Приложение). При расчетах следует учитывать, что Ф(-r)=1-Ф(r).

Ответим, например, на следующий вопрос: какова вероятность того, что в рассматриваемом нами примере доходность r_t будет отклоняться от ожидаемого (среднего) значения на 5 %, т.е. какова вероятность того, что доходность будет лежать в пределах [4,75%; 14,75%]? Воспользуемся формулой (1.6):

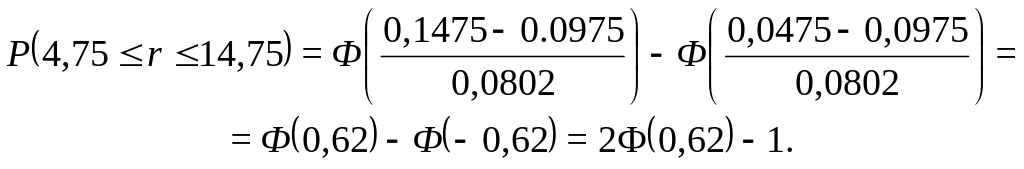
По таблице находим, что Ф(0,62)=0,7324, т.е. Вероятность:

Отталкиваясь от формулы (1.6), можно показать, что с ростом величины σ вероятность попадания нормы отдачи r в заданный интервал уменьшается, т. е. увеличение среднеквадратичного отклонения повышает неопределенность и степень риска инвестиций.