
- •1 Вопрос.
- •2 Вопрос.
- •Вопрос 4 Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы а вычеркиванием I-й строки и j-го столбца.
- •Вопрос 5
- •Свойства обратной матрицы
- •14.Расстояние между двумя точками. Деление отрезка в данном отношении
- •15. Расстояние от точки до прямой
- •16. Уравнение прямой на плоскости
- •19)Числовая последовательность. Определение предела числовой последовательности
14.Расстояние между двумя точками. Деление отрезка в данном отношении
Расстояние d между
двумя точками ![]() (
(![]() ,
, ![]() ,
, ![]() )
и
)
и ![]() (
(![]() ,
, ![]() ,
, ![]() )
в пространстве определяется формулой
)
в пространстве определяется формулой
![]() .
.
Координаты x,
y, z точки
М, которая делит отрезок ![]() ,
ограниченный точками
(
,
,
)
и
(
,
,
),
в отношении
,
ограниченный точками
(
,
,
)
и
(
,
,
),
в отношении ![]() ,
определяется по формулам
,
определяется по формулам
![]() ,
, ![]() ,
, ![]() .
.
В
частности, при ![]() имеет
координаты середины данного отрезка:
имеет
координаты середины данного отрезка:
![]() ,
, ![]() ,
, ![]() .
.
15. Расстояние от точки до прямой
Расстояние d от
данной точки ![]() до
прямой l (под
этим расстоянием понимается длина
перпендикуляра, опущенного из
точки
до
прямой l (под
этим расстоянием понимается длина
перпендикуляра, опущенного из
точки ![]() на
прямую l ),
заданной уравнением А
х + B
y + С =
0, определяется по формуле
на
прямую l ),
заданной уравнением А
х + B
y + С =
0, определяется по формуле ![]()
16. Уравнение прямой на плоскости
Общее
уравнение прямой:
Ах
+ Ву + С = 0 ,
где А и В
не равны нулю одновременно.
Коэффициенты А и В являются
координатами нормального
вектора прямой
( т.е.
вектора, перпендикулярного прямой ).
При А = 0
прямая параллельна оси ОХ ,
при В = 0
прямая параллельна
оси ОY .
При В ![]() 0 получаем уравнение
прямой с угловым коэффициентом:
0 получаем уравнение
прямой с угловым коэффициентом:
![]() Уравнение
прямой, проходящей через точку
( х0 , у 0 )
и не параллельной оси OY,
имеет вид:
у – у 0 = m ( x – х0 )
,
где m – угловой
коэффициент,
равный тангенсу угла, образованного
данной прямой и положительным направлением
оси ОХ .
При А
0, В
0
и С
0 получаем уравнение
прямой в отрезках на осях:
Уравнение
прямой, проходящей через точку
( х0 , у 0 )
и не параллельной оси OY,
имеет вид:
у – у 0 = m ( x – х0 )
,
где m – угловой
коэффициент,
равный тангенсу угла, образованного
данной прямой и положительным направлением
оси ОХ .
При А
0, В
0
и С
0 получаем уравнение
прямой в отрезках на осях:
![]() где a =
– C / A , b =
– C / B .
Эта прямая проходит через точки ( a,
0 )
и ( 0, b ),
т.е. отсекает на осях координат отрезки
длиной a
и b .
Уравнение
прямой, проходящей
через две различные точки ( х1, у 1 )
и ( х2, у 2 ):
где a =
– C / A , b =
– C / B .
Эта прямая проходит через точки ( a,
0 )
и ( 0, b ),
т.е. отсекает на осях координат отрезки
длиной a
и b .
Уравнение
прямой, проходящей
через две различные точки ( х1, у 1 )
и ( х2, у 2 ):
![]() Уравнение
прямой, проходящей через точку
перпендикулярно вектору
нормали.
А(x-x0)+B(y-y0)=0
Уравнение
прямой, проходящей через точку
перпендикулярно вектору
нормали.
А(x-x0)+B(y-y0)=0
17.
Определение. Линией
(кривой) второго порядка называется линия общее
уравнение которой имеет следующий
вид
![]() .
Уравнение
второй степени вида
.
Уравнение
второй степени вида ![]() (не
содержащее члена
(не
содержащее члена ![]() c
произведением координат) называется
пятичленным уравнением кривой
второго порядка. Оно определяет на
плоскости
c
произведением координат) называется
пятичленным уравнением кривой
второго порядка. Оно определяет на
плоскости ![]() эллипс,
гиперболу и параболу (с возможными
случаями распада и вырождения этих
кривых) с осями симметрии, параллельными
осям координат, в зависимости от знака
произведения коэффициентов
эллипс,
гиперболу и параболу (с возможными
случаями распада и вырождения этих
кривых) с осями симметрии, параллельными
осям координат, в зависимости от знака
произведения коэффициентов ![]() и
и ![]() .
В уравнение
окружности (x
– a)2 +
(y – b)2 =
R2,
где (a;
b) —
координаты центра, а R —
радиус окружности.
Пример
1. Найти
координаты центра и радиус окружности,
если ее уравнение задано в виде: 2x2 +
2y2 –
8x +
5y –
4 = 0.
Решение:
Для нахождения
координат центра и радиуса окружности
данное уравнение необходимо привести
к виду, указанному выше в п.9. Для этого
выделим полные квадраты: x2 + y2 –
4x +
2,5y –
2 = 0;
x2 –
4x +
4 –4 + y2 +
2,5y +
25/16 – 25/16 – 2 = 0; (x –
2)2 +
(y +
5/4)2 –
25/16 – 6 = 0;
(x –
2)2 +
(y +
5/4)2 =
121/16. Отсюда находим О(2; -5/4); R = 11/4.
.
В уравнение
окружности (x
– a)2 +
(y – b)2 =
R2,
где (a;
b) —
координаты центра, а R —
радиус окружности.
Пример
1. Найти
координаты центра и радиус окружности,
если ее уравнение задано в виде: 2x2 +
2y2 –
8x +
5y –
4 = 0.
Решение:
Для нахождения
координат центра и радиуса окружности
данное уравнение необходимо привести
к виду, указанному выше в п.9. Для этого
выделим полные квадраты: x2 + y2 –
4x +
2,5y –
2 = 0;
x2 –
4x +
4 –4 + y2 +
2,5y +
25/16 – 25/16 – 2 = 0; (x –
2)2 +
(y +
5/4)2 –
25/16 – 6 = 0;
(x –
2)2 +
(y +
5/4)2 =
121/16. Отсюда находим О(2; -5/4); R = 11/4.
19)Числовая последовательность. Определение предела числовой последовательности
Определение. Числовая последовательность.
Пусть
множество ![]() —
это либо множество вещественных чисел
—
это либо множество вещественных чисел ![]() ,
либо множество комплексных чисел
,
либо множество комплексных чисел ![]() .
Тогда последовательность
.
Тогда последовательность ![]() элементов
множества
называется числовой
последовательностью.
элементов
множества
называется числовой
последовательностью.
Подпоследовательность последовательности ![]() —
это последовательность
—
это последовательность ![]() ,
где
,
где ![]() —
возрастающая последовательность
элементов множества натуральных чисел.
—
возрастающая последовательность
элементов множества натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Свойства
1)Всякая последовательность является своей подпоследовательностью.
2)Для
всякой подпоследовательности ![]() верно,
что
верно,
что ![]() .
.
3)Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
4)Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
5)Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
6)Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
7)Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом.
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Предел
числовой последовательности — предел
последовательности элементов
числового пространства. Числовое
пространство — это метрическое
пространство,
расстояние в котором определяется как
модуль разности между элементами.
Поэтому,предел числовой последовательности —
это такое число, что для всякой сколь
угодно малой величины существует номер,
начиная с которого уклонение членов
последовательности от данной точки
становится меньше заранее заданной
величины.
Целые и рациональные числа
описываются периодическими
последовательностями приближений, в
то время как иррациональные
числа описываются
непериодическими последовательностями
приближений. В численных
методах,
где используется представление чисел
с конечным числом знаков, особую роль
играет выбор системы приближений.
Критерием качества системы приближений
является скорость сходимости. В этом
отношении, оказываются эффективными
представления чисел в виде цепных
дробей.
Первые
строгие определения предела
последовательности дали Больцано в 1816
году и Коши в 1821
году.
ОПРЕДЕЛЕНИЕ.
Число ![]() называется пределом
числовой последовательности
называется пределом
числовой последовательности ![]() ,
если последовательность
,
если последовательность ![]() является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
является
бесконечно малой, т. е. все её элементы,
начиная с некоторого, по модулю меньше
любого заранее взятого положительного
числа.
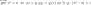 В
случае, если у числовой последовательности
существует предел в виде вещественного
числа
В
случае, если у числовой последовательности
существует предел в виде вещественного
числа ![]() ,
её называют сходящейся к
этому числу. В противном случае,
последовательность называют расходящейся.
Если к тому же она неограниченна, то её
предел полагают равным бесконечности.
,
её называют сходящейся к
этому числу. В противном случае,
последовательность называют расходящейся.
Если к тому же она неограниченна, то её
предел полагают равным бесконечности.
![]() Кроме
того, если все элементы неограниченной
последовательности, начиная с некоторого
номера, имеют положительный знак, то
говорят, что предел такой последовательности
равенплюс
бесконечности.
Кроме
того, если все элементы неограниченной
последовательности, начиная с некоторого
номера, имеют положительный знак, то
говорят, что предел такой последовательности
равенплюс
бесконечности.
![]() Если
же элементы неограниченной
последовательности, начиная с некоторого
номера, имеют отрицательный знак, то
говорят, что предел такой последовательности
равен минус
бесконечности.
Если
же элементы неограниченной
последовательности, начиная с некоторого
номера, имеют отрицательный знак, то
говорят, что предел такой последовательности
равен минус
бесконечности.
![]()
Частичный предел последовательности — это предел одной из её подпоследовательностей.
Верхний предел последовательности — это наибольшая из её предельных точек.
Нижний предел последовательности — это наименьшая из её предельных точек.
ОБОЗНАЧЕНИЯ.
Тот
факт, что последовательность
сходится
к числу
обозначается
одним из следующих способов:
![]() или
или
![]()
20)Число
e
как предел числовой
последовательности.
Определение.
Числом
е
(вторым замечательным пределом)
называется предел числовой
последовательности
![]() .Число
е,
указанное в правой части равенства,
является иррациональным
.Число
е,
указанное в правой части равенства,
является иррациональным
![]()
Второй замечательный предел имеет вид:
![]() или
или ![]() .
В
случае второго замечаельного предела
имеем дело с неопределенностью вида
единица в степени бесконечность
.
В
случае второго замечаельного предела
имеем дело с неопределенностью вида
единица в степени бесконечность ![]() .ЗАМЕЧАНИЕ.
Неопределнность единица в степени
бесконечность
является степенной неопределенностью,
так что может быть раскрыта по правилам
нахождения пределов
показательно степенных функций.
.ЗАМЕЧАНИЕ.
Неопределнность единица в степени
бесконечность
является степенной неопределенностью,
так что может быть раскрыта по правилам
нахождения пределов
показательно степенных функций.
Следствия.
![]()
![]()
![]()
![]()
![]() для
для ![]() ,
, ![]()
![]() 21.
Числовая
последовательность может иметь только
один предел
Сходящаяся числовая
последовательность ограничена
Если
последовательность
21.
Числовая
последовательность может иметь только
один предел
Сходящаяся числовая
последовательность ограничена
Если
последовательность ![]() сходится
к числу а,
то и любая подпоследовательность этой
последовательности сходится к этому
же числу
Если последовательность
сходится
к числу
сходится
к числу а,
то и любая подпоследовательность этой
последовательности сходится к этому
же числу
Если последовательность
сходится
к числу ![]() ,
то, начиная с некоторого номера,
определена последовательность
,
то, начиная с некоторого номера,
определена последовательность ![]() ,
которая является ограниченной.
,
которая является ограниченной.
23.
Первым
замечательным пределом называется
предел
![]()
Вторым
замечательным пределом называется
предел
![]()
Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов. 24. Непрерывность функции в точке Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0). Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
25.
Определение
1. Функция f(x) называется
непрерывной в точке х = а, если она
определена в некоторой двусторонней
окрестности этой точки, включая и саму
эту точку, и при этом
![]() Функция
называется непрерывной на промежутке,
если она непрерывна во всех точках
этого промежутка.
Элементарные
функции — функции,
которые можно получить с помощью
конечного числа арифметических действий
и композицийиз
следующих основных элементарных
функций:
алгебраические:
степенная;
рациональная.
трансцендентные:
показательная и логарифмическая;
тригонометрические и обратные
тригонометрические.
Функция
называется непрерывной на промежутке,
если она непрерывна во всех точках
этого промежутка.
Элементарные
функции — функции,
которые можно получить с помощью
конечного числа арифметических действий
и композицийиз
следующих основных элементарных
функций:
алгебраические:
степенная;
рациональная.
трансцендентные:
показательная и логарифмическая;
тригонометрические и обратные
тригонометрические.
26. Теорема (первая теорема Больцано-Коши) Если функция непрерывна на I и в 2 его точках a иbпринимает значения разных знаков, то по крайней мере в одной точке c между a и b функция обращается в нуль, т.е. f(c)=0 Геометрический смысл: График непрерывной на промежутке и принимающей в двух точках этого промежутка значения разных знаков пересекает ось абсцисс по крайней мере в одной точке.
f(a)<0,f(b)>0,f(c)=0 В теореме лишь утверждается существование нуля функции такой точки c, гдеf(c)=0, но не показывает метода нахождения точки.
27. Теорема (вторая теорема Больцано - Коши) Если f непрерывна на I и в двух его точках a иbf(a)=A>B=f(b), то для всякой точки C∈[B,A] между точками a и b найдется хотя бы одна точкаc, чтоf(c)=C. Геометрический смысл этой теоремы: всякая прямаяy=C, где B<C<A, пересечет график функции fпо крайней мере в одной точке.
28.
Теорема
(первая теорема Вейерштрасса)
Если
функция непрерывна на сегменте, то она
ограничена на нем.
Доказательство:
методом от противного, воспользуемся
свойством замкнутости сегмента [a;b].
Из любой последовательности (xn) этого
сегмента можем выделить
подпоследовательность xnk,
сходящуюся к x0∈[a;b] .
Пусть f не
ограничена на сегменте [a;b],
например, сверху, тогда для всякого
натуральногоn∈N найдется
точка xn∈[a;b] ,
что f(xn)>n.
Придавая n значения
1,2,3,{\ldots}, мы получим последовательность (xn)точек
сегмента [a;b],
для которых выполнено
свойство f(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n...
Последовательность (xn) ограничена
и поэтому из нее по теореме можно
выделить подпоследовательность(xnk),
которая сходится к
точке x0∈[a;b] : limk→∞xnk=x0.
29.
Теорема
(вторая теорема Вейерштрасса)
Если
функция непрерывна на сегменте, то она
достигает на нем своих граней (т.е.
непрерывная на сегменте функция
принимает свое наибольшее и наименьшее
значения).
Доказательство:
Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x).
По первой
теореме
Вейерштрасса c,d∈R .
Докажем, что f достигает
на [a;b] своих
граней, т.е. найдутся такие точки x1,x2∈[a;b] ,
чтоf(x1)=c,f(x2)=d.
Докажем,
например, существование точки x2.
По
определению верхней грани имеем
(∀x∈[a;b])(f(x)=d)
. Предположим противное, т.е. точки x2,
в которой f(x2)=dна
[a;b],
тогда на [a;b]
выполняется условиеf(x)<d
или d−f(x)>0
. Далее введем вспомогательную функцию
ϕ(x)=1d−f(x)
. ϕ(x)
на [a;b]
положительна и непрерывна (как отношение
двух непрерывных на [a;b]
функций и d−f(x)/=0)
, поэтому по первой Т. Вейерштрасса ϕ(x)
на [a;b]
ограничена.
Это означает, что при
некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M)
, отсюда имеем f(x)≤d−1M<d
.
Полученное неравенство противоречит
тому, что d
является верхней гранью функции f(x)
на [a;b],
т.е. наименьшим из верхних границ.
Полученное противоречие и означает
существование точки x2
такой, что f(x2)=d.
30.
Классификация
точек разрыва функции
Все
точки разрыва функции разделяются
на точки
разрыва первого и второго рода.
Говорят,
что функция f (x) имеет точку
разрыва первого рода при x
= a,
если в это точке
Существуют
левосторонний предел ![]() и
правосторонний предел
и
правосторонний предел ![]() ;
Эти
односторонние пределы конечны.
При
этом возможно следующие два
случая:
Левосторонний
предел и правосторонний предел равны
друг другу:
;
Эти
односторонние пределы конечны.
При
этом возможно следующие два
случая:
Левосторонний
предел и правосторонний предел равны
друг другу:
![]() Такая
точка называется точкой
устранимого разрыва.
Левосторонний
предел и правосторонний предел не равны
друг другу:
Такая
точка называется точкой
устранимого разрыва.
Левосторонний
предел и правосторонний предел не равны
друг другу:
![]() Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
Функция f (x) имеет точку
разрыва второго рода при x
= a,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
называется скачком
функции.
Функция f (x) имеет точку
разрыва второго рода при x
= a,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
31.
Это
предел отношения приращения функции
к приращению аргумента, когда приращение
аргумента стремится к нулю.
Геометрический
смысл - тангенс угла касательной с осью
иксов. Физический смысл - производная
от пути по времени есть скорость,
производная от скорости по времени
есть ускорение
33.
Производная сложной функции
Если
функции ![]()
![]()
![]() имеют
конечные производные
имеют
конечные производные ![]() и
и ![]() ,
то
,
то ![]()
![]() .
Значком внизу обозначена переменная,
по которой вычисляется
производная.
34
Производная
степенно-показательной функции
Если
функции
.
Значком внизу обозначена переменная,
по которой вычисляется
производная.
34
Производная
степенно-показательной функции
Если
функции ![]() и
и ![]() имеют
конечные производные, то
имеют
конечные производные, то
![]()
![]()
![]()
![]() 35.
Теорема
Коши́ о среднем значении.
35.
Теорема
Коши́ о среднем значении.
Пусть
даны две функции
|
36.Ферм y=f(x) определенна на (a;b) и во внутренней точке этого промежутка С принимает своё наибольшее или наименьшее значение ,если в этой точке существует ниаменьшая производная,то она равна 1. 37.Ролль Пусть функция y=f(x) определена и непрерывная на [a;b] и дифференциируемая на (a;b),на концах этого промежутка функция принимает равные значения, тогда существует С такая, что f'(C) = 0
38 Теорема.
Пусть функция ![]() дифференцируема в открытом промежутке
дифференцируема в открытом промежутке
![]() и сохраняет непрерывность на концах
этого промежутка. Тогда существует
такая точка
и сохраняет непрерывность на концах
этого промежутка. Тогда существует
такая точка ![]() ,
что
,
что
|
|
(13) |
|
Доказательство. Рассмотрим вспомогательную функцию
![]()
Эта
функция непрерывна и дифференцируема
в промежутке ![]() ,
а на его концах принимает одинаковые
значения:
,
а на его концах принимает одинаковые
значения:
![]()
Тогда
![]() удовлетворяет всем условиям теоремы
Ролля и, следовательно, существует
точка
,
в которой производная функции
равна нулю:
удовлетворяет всем условиям теоремы
Ролля и, следовательно, существует
точка
,
в которой производная функции
равна нулю:
![]()
Следствие
1.
В частном случае, когда ![]() ,
из теоремы Лагранжа вытекает, что
существует точка
,
в которой производная функции
равна
нулю:
,
из теоремы Лагранжа вытекает, что
существует точка
,
в которой производная функции
равна
нулю: ![]() .
Это означает, что теорема Лагранжа
является обобщением теоремы
Ролля.
Следствие
2.
Если
.
Это означает, что теорема Лагранжа
является обобщением теоремы
Ролля.
Следствие
2.
Если ![]() во всех точках некоторого промежутка
,
то
во всех точках некоторого промежутка
,
то ![]() в
этом промежутке.
Действительно, пусть
в
этом промежутке.
Действительно, пусть ![]() и
и ![]() – произвольные точки промежутка
и
– произвольные точки промежутка
и ![]() .
Применяя теорему Лагранжа к промежутку
.
Применяя теорему Лагранжа к промежутку
![]() ,
получим
,
получим
![]()
Однако во всех точках промежутка . Тогда
![]()
Учитывая
произвольность точек
и
,
получаем требуемое
утверждение.
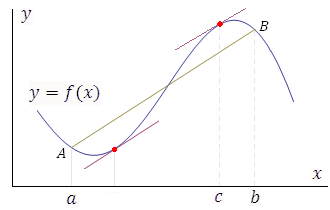
Геометрическая
интерпретация теоремы Лагранжа.
Разностное отношение в правой части
формулы (13) есть угловой коэффициент
секущей, проходящей через точки ![]() и
и ![]() ,
а производная
,
а производная ![]() равна угловому коэффициенту касательной
к графику функции
равна угловому коэффициенту касательной
к графику функции ![]() в некоторой средней точке промежутка
.
Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
в некоторой средней точке промежутка
.
Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
39.40
Теорема (правило Лопиталя).
Пусть функции f(x) и g(x) дифференцируемы
в некоторой окрестности точки a,
за исключением, быть может, самой
точки a,
и пусть ![]() или
или ![]() .
Тогда, если существует предел отношения
производных этих функций
.
Тогда, если существует предел отношения
производных этих функций ![]() ,
то существует и предел отношения самих
функций f(x)/g(x) при x→а, причем
,
то существует и предел отношения самих
функций f(x)/g(x) при x→а, причем
|
(1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
41.
Неопределенности
типа ![]() Пусть
заданы две функции f (x) и g (x),
такие, что
Пусть
заданы две функции f (x) и g (x),
такие, что![]() В
этом случае говорят, что функция
В
этом случае говорят, что функция ![]() имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
Неопределенности
типа
имеет
неопределенность типа
в
точке x
= a.
Чтобы найти предел при x
= a когда
функция
содержит
неопределенность
,
нужно разложить на множители числитель
и/или знаменатель и затем сократить
члены, стремящиеся к нулю.
Примечание:
В данном разделе при вычислении пределов
не используется правило
Лопиталя.
Неопределенности
типа ![]() Пусть
две функции f (x) и g (x) обладают
свойством
Пусть
две функции f (x) и g (x) обладают
свойством
![]() где a является
действительным числом, либо стремится
к +
∞ или − ∞. Говорят,
что в этом случае функция
имеет
в точке a неопределенность
типа
.
Для вычисления предела в этой точке
необходимо разделить числитель и
знаменатель на x в
наивысшей степени.
Неопределенности
типа
где a является
действительным числом, либо стремится
к +
∞ или − ∞. Говорят,
что в этом случае функция
имеет
в точке a неопределенность
типа
.
Для вычисления предела в этой точке
необходимо разделить числитель и
знаменатель на x в
наивысшей степени.
Неопределенности
типа ![]() Неопределенности
этих типов сводятся к рассмотренным
выше неопределенностям типа
и
.
Неопределенности
этих типов сводятся к рассмотренным
выше неопределенностям типа
и
.
42. Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда отрицательное, либо всегда положительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции 43. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x= x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
44.
АСИМПТОТЫ
ГРАФИКА ФУНКЦИИ
При
исследовании функции важно установить
форму ее графика при неограниченном
удалении точки графика от начала
координат.
Особый интерес представляет
случай, когда график функции при удалении
его переменной точки в бесконечность
неограниченно приближается к некоторой
прямой.
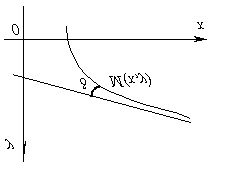
 Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем
стремлении в бесконечность должна
неограниченно приближаться к
асимптоте.
Кривая может приближаться
к своей асимптоте, оставаясь с одной
стороны от нее или с разных сторон,
бесконечное множество раз пересекая
асимптоту и переходя с одной ее стороны
на другую.
Если обозначим через d
расстояние от точки M кривой
до асимптоты, то ясно, что d стремится
к нулю при удалении точки M в
бесконечность.
Будем в дальнейшем
различать асимптоты вертикальные и
наклонные.
Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем
стремлении в бесконечность должна
неограниченно приближаться к
асимптоте.
Кривая может приближаться
к своей асимптоте, оставаясь с одной
стороны от нее или с разных сторон,
бесконечное множество раз пересекая
асимптоту и переходя с одной ее стороны
на другую.
Если обозначим через d
расстояние от точки M кривой
до асимптоты, то ясно, что d стремится
к нулю при удалении точки M в
бесконечность.
Будем в дальнейшем
различать асимптоты вертикальные и
наклонные.
ВЕРТИКАЛЬНЫЕ
АСИМПТОТЫ
Пусть
при x→ x0 с
какой-либо стороны функция y = f(x)неограниченно
возрастает по абсолютной величине,
т.е. ![]() или
или ![]() или
или ![]() .
Тогда из определения асимптоты следует,
что прямая x = x0 является
асимптотой. Очевидно и обратное, если
прямая x = x0 является
асимптотой, т. о.
.
Таким
образом, вертикальной асимптотой
графика функции y
= f(x) называется
прямая, если f(x) →
∞ хотя бы при одном из условий x→ x0 –
0 или x → x0 +
0, x = x0
Следовательно,
для отыскания вертикальных асимптот
графика функции y = f(x) нужно
найти те значения x = x0,
при которых функция обращается в
бесконечность (терпит бесконечный
разрыв). Тогда вертикальная асимптота
имеет уравнение x = x0.
.
Тогда из определения асимптоты следует,
что прямая x = x0 является
асимптотой. Очевидно и обратное, если
прямая x = x0 является
асимптотой, т. о.
.
Таким
образом, вертикальной асимптотой
графика функции y
= f(x) называется
прямая, если f(x) →
∞ хотя бы при одном из условий x→ x0 –
0 или x → x0 +
0, x = x0
Следовательно,
для отыскания вертикальных асимптот
графика функции y = f(x) нужно
найти те значения x = x0,
при которых функция обращается в
бесконечность (терпит бесконечный
разрыв). Тогда вертикальная асимптота
имеет уравнение x = x0.
Примеры.
Найти
вертикальные асимптоты графика
функции ![]() .
Так
как
.
Так
как ![]() ,
то прямая x =
2 является вертикальной
асимптотой.
,
то прямая x =
2 является вертикальной
асимптотой.
![]() .
Прямая x =
0 – вертикальная асимптота.
.
Прямая x =
0 – вертикальная асимптота.
НАКЛОННЫЕ
АСИМПТОТЫ
Поскольку
асимптота – это прямая, то если
кривая y = f(x) имеет
наклонную асимптоту, то ее уравнение
будет y = kx + b.
Наша задача найти коэффициенты k и b.
Теорема.
Прямая y = kx + b служит
наклонной асимптотой при x →
+∞ для графика функции y = f(x) тогда
и только тогда, когда ![]() .
Аналогичное утверждение верно и при x →
–∞.
Доказательство.
Пусть MP –
длина отрезка, равного расстоянию от
точки M до
асимптоты. По условию
.
Аналогичное утверждение верно и при x →
–∞.
Доказательство.
Пусть MP –
длина отрезка, равного расстоянию от
точки M до
асимптоты. По условию ![]() .
Обозначим через φ угол наклона асимптоты
к оси Ox.
Тогда из ΔMNP следует,
что
.
Обозначим через φ угол наклона асимптоты
к оси Ox.
Тогда из ΔMNP следует,
что ![]() .
Так как φ постоянный угол (φ ≠ π/2), то
.
Так как φ постоянный угол (φ ≠ π/2), то ![]() ,
но
,
но
MN
= MK – NK = y - yас =
f(x) - (kx+b).
Следовательно,
мы можем записать следующее равенство ![]() .
Так
как x →
+∞, то должно выполняться равенство
.
Так
как x →
+∞, то должно выполняться равенство ![]() .
Но при постоянных k и b
.
Но при постоянных k и b ![]() и
и ![]() Следовательно,
Следовательно, ![]() ,
т.е.
,
т.е. ![]() .
Если
число k уже
известно, то
.
Если
число k уже
известно, то ![]() ,
поэтому
,
поэтому ![]() .
Для
доказательства в случае x →
–∞ все рассуждения аналогичны.
.
Для
доказательства в случае x →
–∞ все рассуждения аналогичны.
45.
Необходимое
условие экстремума
Функция
g(x) в точке![]() имеет
экстремум(максимум или минимум), если
функция определена в двухсторонней
окрестности точки
и
для всех точек x некоторой области:
имеет
экстремум(максимум или минимум), если
функция определена в двухсторонней
окрестности точки
и
для всех точек x некоторой области: ![]() ,
выполнено соответственно неравенство
,
выполнено соответственно неравенство
![]() (в
случае максимума) или
(в
случае максимума) или ![]() (в
случае минимума).
Экстремум функции
находиться из условия:
(в
случае минимума).
Экстремум функции
находиться из условия:![]() ,
если производная существует, т.е.
приравниваем первую производную функции
к нулю.
46.Достаточное
условие экстремума
1) Первое
достаточное условие:
Если:
а)
f(x) непрерывная
функция и
определена в некоторой окрестности
точки
такой,
что первая производная в данной
точке равна нулю или не существует.
б)
f(x) имеет конечную производную в
окрестности задания и непрерывности
функции
в) производная сохраняет
определенный знак справа от точки
и
слева от этой же точки, тогда точку
можно
охарактеризовать следующим
образом
2) Второе
достаточное условиe
Если функция g(x)
обладает второй производной
,
если производная существует, т.е.
приравниваем первую производную функции
к нулю.
46.Достаточное
условие экстремума
1) Первое
достаточное условие:
Если:
а)
f(x) непрерывная
функция и
определена в некоторой окрестности
точки
такой,
что первая производная в данной
точке равна нулю или не существует.
б)
f(x) имеет конечную производную в
окрестности задания и непрерывности
функции
в) производная сохраняет
определенный знак справа от точки
и
слева от этой же точки, тогда точку
можно
охарактеризовать следующим
образом
2) Второе
достаточное условиe
Если функция g(x)
обладает второй производной![]() причем
в некоторой точке
первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка
экстремум
функции g(x),
причем если
причем
в некоторой точке
первая
производная равна нулю, а вторая
производная отлично от нуля. Тогда
точка
экстремум
функции g(x),
причем если ![]() ,
то точка является максимумом; если
,
то точка является максимумом; если ![]() ,
то точка является минимумом.
,
то точка является минимумом.
3) Третье достаточное условие Пусть функция g(x) имеет в некоторой окрестности точки N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:
а)
Если N - четно, то точка
экстремум
функции:![]() у
функции точка максимума,
у
функции точка максимума, ![]() у
функции точка минимума.
у
функции точка минимума.
б) Если N - нечетно, то в точке у функции g(x) экстремума нет.
47.
