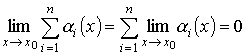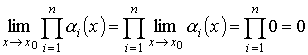45. Предел функции.

Будем называть окрестности точки x0 любой интервал, содержащий эту точку (рисунок: на прямой со стрелочкой точка х0 и по обе стороны от неё взяты @ и B).

б(наоборот) - окрестность этой точки; х0 - этот интервал

Пусть функция y = f(x), определена в некоторой окрестности точки х0 за исключением может быть самой точки. Выберем произвольным образом некоторую последовательность {xn}, xn (неравно) x0, которая сходится к х0, т.е. lim(n->бесконечности) xn = x0. Вычислим значения функции, в каждой точке xn и построим последовательность yn : yn = f(xn).

Если для любой последовательности сходится к y0, соответственная последовательность yn сходится и все такие последовательности имеют один и тот же предел, то число B называется пределом функции y = f(x), при x -> x0 и обозначается : lim(при x -> x0) = в <=> А(наоборот)E(эпсилон) > 0, З б(наоборот) > 0, A(наоборот)x : |x -x0| < б(наоборот) => |f(x) - в| < E(эпсилон) В определении нужно отметить, что величина предела не зависит то того, что определена функция в самой точке или нет.

Геометрический смысл производной

.

Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е.

где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.

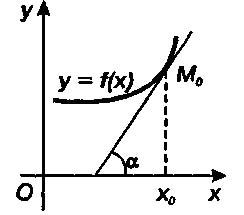
Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид

Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линииу = f(x) в точке Мо(хо, уо) запишется так:

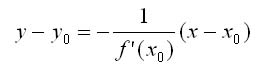
46.

Бесконечно малые функции

  Функция f (x) называется бесконечно малой функцией в точке х = х₀, если

Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x₀ – 0, x → x₀ + 0.   Можно дать равносильное определение бесконечно малой функции «на языке ε – δ: функция f (x) называется бесконечно малой в точке х = х₀, если для любого как угодно малого ε > 0 существует δ = δ(ε) > 0, такое, что для всех х, удовлетворяющих неравенству 0 < | х – x₀ | < δ, выполняется неравенство | f (x) | < ε. Или в символьном виде

(  ε > 0) (   δ = δ(ε) > 0)(   0 < |х – х₀| < δ ) : | f (x) | < ε.

   Имеет место следующая теорема: функция f (x) в окрестности точки х₀ отличается от своего предельного значения A на бесконечно малую функцию.   Доказательство. Пусть

Рассмотрим разность f (x) – А = α(х). Так как

,

то функция α(х) является бесконечно малой при x → х₀.

Свойства бесконечно малых функций

  Опираясь на правила вычисления пределов, можно сформулировать свойства бесконечно малых: алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x₀, а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x₀:

1.
2.
3.
4.

  Все сказанное о бесконечно малых функциях при x → x₀ справедливо и для бесконечно малых функций при x → ∞, x → + ∞, x → – ∞, x → x₀ – 0, x → x₀ + 0.

47.-----------

48. Первый замечательный предел. lim (x -> x0) sinx/x = 1 Доказательство: Возьмём круг R = 1. Обозначим радианную меру угла МОВ через х. Пусть 0 < x < П/2. Сравним S(треуг-ка МOB) с сектором МОВ и S(треуг-ка ОВС), очевидно, что S(треуг-ка МОВ), меньше S сектора МОВ и меньше S(треуг-ка МОВ). S(треуг-ка МОВ) < S(сект МОВ) < S(треуг-ка ОВС) ; S(треуг-ка МОВ) = 1/2 |OB| * |OM| * sinx = 1/2 sinx ; S(сектора) = x/2 * |OB|^2 = 1 * x/2 = x/2 ; S(треуг-ка ОВС) = 1/2 |OB| * |OC| = 1/2 BC = 1/2 tgx 1/2 sinx < x/2 < 1/2 tgx ; sinx/sinx < x/sinx< tgx/sinx ; 1 < x/sinx < 1/cosx ; cosx < sinx/x < 1 ; lim(x -> 0) cosx = 1 ; lim(x ->0) 1 = 1 => lim(x -> 0) sinx/x = 1 Пусть x < 0 ; (-x) > 0 ; sinx/x = sin(-x)/-x lim(x -> 0) sin(-x)/-x = (определитель в нём 1-ая стока -x = t ; 2-ая строка x ->0 ; 3-ая строка t ->0) = lim (t -> 0) sint/t = 1

49. Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называетсядифференци́рованием.

Определение  Править

Пусть в некоторой окрестности точки   определена функция  Производной функции   в точке   называется предел, если он существует,

Производная функции в точке   обозначается символами

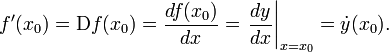
50. Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔxΔy

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k  Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

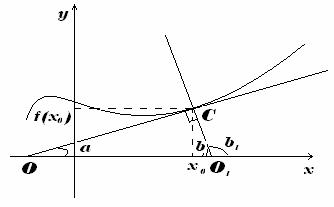
Уравнение нормали

Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).