Определение

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Частичный предел последовательности — это предел одной из её подпоследовательностей.

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.

Обозначения

Тот факт, что последовательность   сходится к числу   обозначается одним из следующих способов:

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

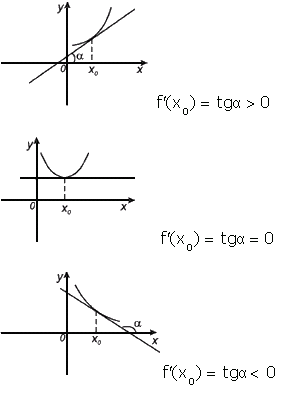
Рассмотрим график функции y = f ( x ):

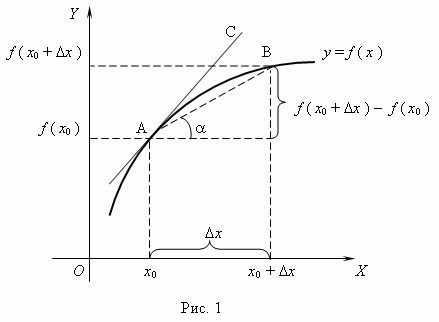
Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

43. "Единственность предела числовой последовательности"

Определение: Если последовательность an имеет предел, то этот предел единственный. Используются 3 основных стиля:

Доказательство(от противного): Допустим, что этот предел не единственный, т.е. существует 2-а предела последовательности, отличных друг от друга : lim(при n -> к бесконечности) an = в1 ; lim(при n -> к бесконечности) an = в2 ; в1 = в2 Рассмотрим число А = (в1 + в2)/2 (рисунок на прямой со стрелочкой взят отрезок в1в2 и А - середина отрезка) В1 < A, тогда найдётся номер №1 ; A(наоб-т)n > №1 : an < A (по свойству если дана последовательность an lim (n стремится к бесконечности) an = в, в>@, то начиная с некоторого номера все члены будут меньше @). в2>A, тогда найдётся номер №2, такой что для любого n > №2 выполняется неравенство : an > A. Пусть № = max {№1 ; №2}, и для любого n > №, выполянются оба неравенства одновременно, следовательно, для любого члена любого члена последовательности выполняется неравенство: A < an < A -а это противоречие.

Свойство №1: Пусть дана последовательность an lim (n стремится к бесконечности) an = в, в>@, то начиная с некоторого номера все члены последовательности будут меньше @). Следствие: Если в > B, то начиная с некоторого номера, все члены последовательности будут больше B. Если @ < в < B, то начиная с некоторого номера все члены последовательности будут удовлетворять неравенству : @ < an < B

Свойство №2:"Ограниченность последовательности имеющей предел": Если lim(n стремящаяся к бесконечности) an = в, то последовательность является ограниченной и для всех её членов выполянется неравенство @ < an < B.

Теоремы о пределах: пусть имеются 2-е последовательности {an}, {вn} => lim(n стремится к бесконечности)an = a ; lim(n стремится к бесконечности) вn = в

-lim(n стремится к бесконечности) (an + вn) = lim(n стремится к бесконечности) an + lim(n стремится к бесконечности) вn = a + в -lim(n стремится к бесконечности) (an + вn) = lim(n стремится к бесконечности) an + lim(n стремится к бесконечности) вn = a - в -lim(n стремится к бесконечности) (an * вn) = lim(n стремится к бесконечности) an * lim(n стремится к бесконечности) вn = a * в -lim(n стремится к бесконечности) (an / вn) = lim(n стремится к бесконечности) an / lim(n стремится к бесконечности) вn = a / в

44. Бесконечно - малые последовательности

Определение 1. Последовательность   называется бесконечно-малой последовательностью, если  , т.е. если

.

Определение 2. Последовательность   называется бесконечно-большой последовательностью, если   (это записывается еще и так:  , не учитывая знака перед  ), т.е. если

.

Изучим некоторые свойства этих последовательностей.

1⁰. Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.

Доказательство:

 - б.м.п. =>

 - б.м.п. =>

Возьмем . Тогда

откуда следует, что  есть б.м.п.

Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п

2⁰. Произведение б.м.п на ограниченную последовательность есть б.м.п.

Доказательство:

 - ограничена. =>

 - б.м.п. =>

.

Но тогда 

отсюда и следует, что   есть б.м.п.

3. Б.м.п. ограничена

Доказательство:

Пусть   - б.м.п. Тогда  .

Возьмем  .

Тогда   т.е.   ограничена.

Следствие. Произведение б.м.п. есть также б.м.п.

4. Пусть   - б.м.п. и  . Тогда   есть б.б.п.

Доказательство:

 - б.м.п =>  .

Возьмем любое   и положим  .

Тогда 

отсюда следует, что   есть б.б.п.

5. Пусть   - б.б..п, тогда   есть б.м.п.

 - б.б.п =>  .

Возьмем любое   и положим 

Тогда 

отсюда следует, что   есть б.м.п.

свойства бесконечно малых последовательностей

   Теорема.Сумма (разность) двух бесконечно малых последовательностей есть бесконечно малая последовательность.   Доказательство. Пусть {α_n} и {β_n} — бесконечно малые последовательности. Требуется доказать, что последовательность α_n ± β_n тоже бесконечно малая. Пусть ε – произвольное как угодно малое положительное число, N₁– номер, начиная с которого выполняется неравенство

,

N₂ - номер, начиная с которого выполняется неравенство

.

(Такие номера N₁ и N₂ найдутся по определению бесконечно малой последовательности.) Возьмем

N = max {N₁, N₂},

тогда при n > N будут одновременно выполняться два неравенства:

и

Следовательно, при n > N имеем

Это значит, что последовательность

α_n ± β_n

бесконечно малая.   Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.   Теорема 3. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.   Доказательство. Пусть {α_n} и {β_n} — бесконечно малые последовательности. Требуется доказать, что последовательность {α_n·β_n} тоже является бесконечно малой. Так как последовательность {α_n} бесконечно малая, то для любого как угодно малого положительного числа ε> 0 существует номер N₁, зависящий от ε, такой, что для всех последующих номеров n > N₁ ,будет выполнено неравенство

а так как {β_n) – также бесконечно малая последовательность, то для любого как угодно малого положительного числа ε> 0 существует номер N₂, зависящий от ε, такой, что для всех последующих номеров n > N₂ ,будет выполнено неравенство

Возьмём N = max{N₁, N₂}, тогда при n > N будут одновременно выполняться оба неравенства. Следовательно,

Это означает, что последовательность {α_n·β_n} бесконечно малая.   Следствие. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.    Теорема 4.Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.   Доказательство. Пусть {x_n} – ограниченная, а {α_n} – бесконечно малая последовательности. Требуется доказать, что последовательность{x_n·α_n} бесконечно малая. Так как последовательность {x_n} ограничена, то существует число А > 0 такое, что любой элемент числовой последовательности {x_n} удовлетворяет неравенству | x_n| ≤ A. Возьмем любое как угодно малое положительное число ε > 0. Поскольку последовательность {α_n} бесконечно малая, то для любого как угодно малого положительного числа ε/ A существует номер N такой, что при всех n > N выполняется неравенство

 

Следовательно, при n > N имеем

Это означает, что последовательность {x_n·α_n} является бесконечно малой числовой последовательностью.   Следствие. Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.