40. Обратная функция

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

Определение

Функция   является обратной к функции  , если выполнены следующие тождества:

 для всех 

 для всех 

Существование

Чтобы найти обратную функцию, нужно решить уравнение   относительно  . Если оно имеет более чем один корень, то функции обратной к   не существует. Таким образом, функция   обратима на интервале   тогда и только тогда, когда на этом интервале она инъективна.

Для непрерывной функции   выразить   из уравнения   возможно в том и только том случае, когда функция   монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её монотонности. Например,   является обратной функцией к   на  , хотя на промежутке  обратная функция другая:  .

Примеры

Если  , где   то 

Если  , где   фиксированные постоянные и  , то 

Если  , то 

Свойства

Областью определения   является множество  , а областью значений множество  .

По построению имеем:

или

,

,

или короче

,

,

где   означает композицию функций, а   — тождественные отображения на   и   соответственно.

Функция   является обратной к  :

.

Пусть   — биекция. Пусть   её обратная функция. Тогда графики функций   и   симметричны относительно прямой  .

Параметрическое задание функций

Для вычисления сплайн-функции, заданной на сетке x₁ < x₂ < … < x_n, требуется упорядоченная монотонно возраста­ющая последовательность x_i. Это означает, что сплайн-функция y = y(x) может быть построена только для однозначной функции.

Однако, используя параметрическое задание функции, можно построить неоднозначную, в том числе замкнутую, кривую (периоди­ческий сплайн). Для этого выбирается независимая переменная t, удовлетворяющая указанным выше требованиям, и вычисляются сплайн-приближения x(t) и y(t), а затем строится кривая, прохо­дящая через точки (x_i, y_i), соответствующие выбранным t_i.

Предлагается два способа задания параметра t. B простейшем случае t задается как последовательность целых чисел: t_j = j. Другая возможность состоит в том, что t со­от­вет­ству­ет суммарной длине хорд, которая является аппроксимацией длины дуги между первой и j-й точками. B этом случае

и  .

(5.2)

Вычислив приближенно длины отрезков получившейся кривой x = x(t), y = y(t), можно построить более точные сплайны. Одна­ко, это не приводит к заметному изменению самой кри-вой.

41 Числовые последовательности

1. Определение числовой последовательности и способы ее задания.

Что такое числовая последовательность и как она задается, вам известно из курса алгебры 9-го класса. Напомним соответствующее определение.

Определение 1. Функцию вида   называют функцией натурального аргумента или числовой последовательностью и обозначают 

Иногда для обозначения последовательности используется запись (у_n).

Последовательности можно задавать различными способами, например словесно, когда правило задания последовательности описано словами, без указания каких-то формул. Так, словесно задается последовательность простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...

Особенно важны аналитический и рекуррентный способы задания последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее п-го члена.

Приведем три примера.

1)    у_п =п². Это — аналитическое задание последовательности 1,4, 9,16, ...,п², ...

Указав конкретное значение п, нетрудно найти член последовательности с соответствующим номером. Если, например, п =9,   Напротив, если взят определенный член последовательности, можно указать его номер. Например, если у_п =625, то изуравнения п² =625 находим, что п =25. Это значит, что 25-й член заданной последовательности равен 625.

2)    у_п =С. Здесь речь идет о последовательности 

Такую последовательность называют постоянной (или стационарной).

3)    у_п =2ⁿ. Это — аналитическое задание последовательности 

Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить п-й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия — это числовая последовательность (а„), заданная рекуррентно соотношениями:

Геометрическая прогрессия — это числовая последовательность , заданная рекуррентно соотношениями:

 — знаменатель геометрической прогрессии). Прогрессии вы изучали в курсе алгебры 9-го класса.

2. Свойства числовых последовательностей

Числовая последовательность — частный случай числовой функции, а потому некоторые свойства функций (ограниченность, монотонность) рассматривают и для последовательностей.

Определение 2. Последовательность (у„) называют ограниченной сверху, если все ее члены не больше некоторого числа.

Иными словами, последовательность (у„) ограничена сверху, если существует числом такое, что для любого л выполняется неравенство у_n<М. Число М называют верхней границей последовательности.

Например, последовательность -1, -4, -9, -16, ...,-п2, ... ограничена сверху. В качестве верхней границы можно взятьчисло -1 или любое число, которое больше, чем -1, например 0.

Определение 3. Последовательность (у„) называют ограниченной снизу, если все ее члены не меньше некоторого числа.

Иными словами, последовательность (у_n) ограничена снизу, если существует число т такое, что для любого л выполняется неравенство у„>M. Число m называют нижней границей последовательности.

Например, последовательность 1, 4, 9, 16, ..., п2, ... ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1.

Если последовательность ограничена и сверху, и снизу, то ее называют ограниченной. Например,   Эта последовательность ограничена и сверху, и снизу. В качестве верхней границы можно взять число 1, в качестве нижней границы — число 0.

Если построить график последовательности

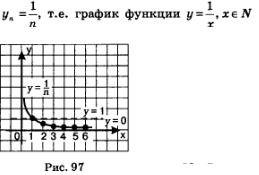 в прямоугольной системе координат, то окажется, что весь он расположен в полосе между некоторыми горизонтальными прямыми, например, у=0, и у = 1 (рис. 97), а в зтом и состоит, как известно, геометрический признак ограниченности функции.

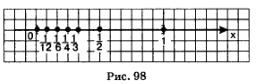
Особенно наглядным становится свойство ограниченности последовательности, если члены последовательности отметить точками на числовой прямой. Ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку. Так, изобразив члены последовательности точками на числовой прямой, замечаем, что все они принадлежат отрезку [0, 1] (рис. 98).

Определение 4. Последовательность (у„) называют возрастающей, если каждый ее член больше предыдущего:

Например, 1, 3, 5, 7.....2n -1,... — возрастающая последовательность.

Определение 5. Последовательность (у„) называют убывающей, если каждый ее член меньше предыдущего: Например,    убывающая последовательность. Возрастающие и убывающие последовательности объединяют общим термином — монотонные последовательности. Приведем еще несколько примеров.  Эта последовательность не является ни возрастающей, ни убывающей (немонотбнная последовательность). 2)    у_n =2ⁿ. Речь идет о последовательности 2, 4, 8, 16, 32, ... Это — возрастающая последовательность. Вообще, если а > 1, то последовательность у_n =аⁿ возрастает. 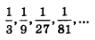Речь идет о последовательности  Это — убывающая последовательность. Вообще, если 0 <а < 1, то последовательность у_n =аⁿ убывает.

.

42. Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,

предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.

Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чиселсуществование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.

Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.^[1] Вчисленных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
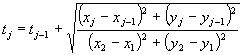