38. Суперпозиция

(позднелат. superpositio, – наложение, от лат. superpositus – положенный наверх) (композиция) – операция логико-математич. исчислений, заключающаяся в получении из к.-л. данных функций f и g данного исчисления новой функции g (f) (выражение g (f(x)) означает при этом результат применения функциональной операции g к результату применения функциональной операции f к аргументу x – при выполнении естеств. условия, что область значений f включает в себя область определения g, или, короче, просто gf). С., заключающаяся в повторном применении о д н о й и т о й ж е функции (операции), наз. обычно и т е р а ц и е й этой функции (операции). Так, операцию умножения часто определяют через итерацию операции сложения, операцию возведения в степень – через итерацию операции умножения и т.п. С. является осн. способом получения формул различных исчислений исходя из к.-л. перечня основных ("элементарных") операций. Так, из "элементарных высказываний" А, В, С., ... логики высказываний и логич. операций , &, / и ⊃ получают посредством С. формулы А, A / B, A / B ⊃ C, (А / В ⊃ С) & А и т.д., и т.п. При описании нек-рых исчислений операцию С. явным образом включают в число допустимых способов образования выражений исчисления в виде т.н. (регулярной) схемы С., или п о д с т а н о в к и; см. Рекурсивные функции и предикаты.

Элементарные функции и их классификация

 

         Функции:

                                                                   - степенная;

                                                      - показательная;

                                        - логарифмическая;

                                                             - тригонометрические;

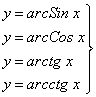                                                         - обратные тригонометрические;

                                                    - постоянная.

 

 Называются основными элементарными функциями.

 

З а м е ч а н и е.

         Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и суперпозиций основных элементарных функций, называется просто элементарнойфункцией.

         Элементарные функции обычно делят на классы:

         1. Многочлены (полиномы) - это функции вида:

        .

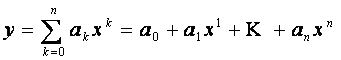Если  , то число   называется степенью данного полинома.

При   многочлен первой степени и называется линейной функцией;

        2. Класс рациональных функций:

              , где   - полиномы;

 3. Алгебраические функции:

Функции, заданные с помощью суперпозиций рациональных функций, степенных с рациональными показателями и четырех арифметических действий, называются алгебраическими.

Например:                     .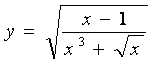

 

39. Монотонность функции

 

Возрастающие и убывающие функции объединяют общим понятием: монотонные функции.

Монотонная функция – это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Говоря иначе, если при возрастании значения x значение y тоже возрастает, то это возрастающая функция.

Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Говоря иначе, если при возрастании значения x значение y убывает, то это убывающая функция.

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Свойства монотонных функций:

1) Сумма нескольких возрастающих функций является возрастающей функцией. 2) Произведение неотрицательных возрастающих функций есть возрастающая функция. 3) Если функция f возрастает и сохраняет знак, то функция 1/f убывает. 4) Если функция f возрастает и неотрицательна, то fn тоже возрастает (n ∈ N). 5) Композиция g (f (x)) возрастающих функций f и g также возрастает. 6) Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает (c – некоторая константа).

 

Производная и монотонность функции.

Зависимость между знаком производной и характером монотонности:

Если на промежутке Х функция возрастает и имеет на нем производную, то производная неотрицательна. Если на промежутке Х функция убывает и имеет на нем производную, то производная неположительна.

 

Условия возрастания или убывания функции y = f(x):

Функция возрастает, если во всех точках открытого промежутка Х производная f ′(x) больше нуля: f ′(x) > 0. Говоря проще, функция возрастает, если производная положительна. Примечание: Равенство f ′(x) = 0 либо выполняется лишь в конечном множестве точек, либо не выполняется вовсе.   Функция убывает, если во всех точках открытого промежутка Х производная f ′(x) меньше нуля: f ′(x) < 0. Говоря проще, функция убывает, если производная отрицательна. Примечание: равенство f ′(x) = 0 либо выполняется лишь в конечном множестве точек, либо не выполняется вовсе.

 

Условие существования постоянной функции:

Функция y = f(x) постоянна на промежутке Х, если во всех точках этого промежутка производная  f ′(x) равна нулю: f ′(x) = 0

 

Монотонность некоторых функций:

Функция	Производная	Монотонность
Линейная функция y = ax + b	y' = a	При a > 0 возрастает При a < 0 убывает. При a = 0 постоянна.
Прямая пропорциональность y = kx  (k ≠ 0)	y' = k	При k > 0 возрастает. При k < 0 убывает.
Обратная пропорциональность                      k             y = ——   (k ≠ 0)                      x	k          y' = – ——                      x2	При k > 0 убывает на (–∞; 0) и (0; +∞). При k < 0 возрастает на (–∞; 0) и (0; +∞)
Квадратичная функция y = ax2 + bx + c	y' = 2ax + b	При a > 0 убывает на (–∞; –b/2a] и возрастает на [–b/2a; +∞). При a < 0 возрастает на (–∞; –b/2a] и убывает на [–b/2a; +∞).
Функция корня y = √x	1            y' = ——                    2√x	Возрастает на промежутке [0; +∞)