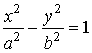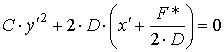Определение

Пусть   — множество и   — множество отображений из A в A. Отображение f из A в множество B называется инвариантом для G, если для любых   и   выполняется тождество  .

Примеры

В теории дифференциальных уравнений инвариантом называется функция, зависящая от искомой функции, значение которой постоянно (первый интеграл).

Теория инвариантов занимается поиском инвариантных многочленов (или просто «инвариантов») и изучением образованной ими алгебры для случая линейных представлений алгебраических групп, а также действий алгебраических групп на алгебраических многообразиях.

35. Классификация линий второго порядка

 В зависимости от знака величины А·С – В2 линии второго порядка разделяются на следующие три типа

эллиптический, А·C – В2 > 0.

гиперболический,А·C – В2 < 0.

параболический,А·C – В2 = 0.

Эллиптический тип

 Согласно лемме, общее уравнение линии второго порядка может быть приведено к виду (для удобства записи опускаем штрихи у коэффициентов и координат)

А·х2 + С·у2 + F = 0.

.

Поскольку А·С – В2 > 0, то возможны следующие случаи:

А > 0, C > 0 (случай A < 0, C < 0 сводится к случаю A > 0, C > 0 умножением уравнения на ( – 1) и F < 0. Перенесем F в правую часть уравнения и разделим на него. Уравнение принимает вид

канонического уравнения эллипса, где а2= − F/A, b = − F/C.

A > 0, C > 0 и F > 0. Тогда, аналогично предыдущему, уравнение можно привести к виду

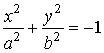
Этому уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением мнимого эллипса.

A > 0, C > 0, F = 0. Уравнение имеет вид (а2 = А, с2 = С): а2·х2 + с2·y2 = 0. Ему удовлетворяют координаты только одной точки х = 0, у = 0. Такое уравнение назовем уравнением пары мнимых пересекающихся прямых.

Гиперболический тип

 Согласно лемме, общее уравнение линии второго порядка приводится к виду А·х2 + С·у2 + F = 0.  Если А > 0, C < 0 (случай A < 0, C > 0 сводится к случаю A > 0, C < 0 умножением уравнения на (– 1) и F ≠ 0. Пусть, например, F< 0. Перенесем F в правую часть уравнения и разделим на него. Уравнение принимает вид

,

где а2 = F/A, b2 = F/C. Полученное уравнение является каноническим уравнением гиперболы.  Если A > 0, C < 0, F = 0, то уравнение имеет вид (а2 = А, с2 = − С): а2·x2−с2·у2 = 0 или (а·х – с·у)·(а·x + b·y) = 0. Последнему уравнению удовлетворяют только координаты точек плоскости, расположенных на прямых а·x + b·y =0, а·x - b·y =0, пересекающихся в начале координат, и, таким образом, в этом случае имеем пару пересекающихся прямых.

Параболический тип

 Если А·С – В2 = 0, то, как и в лемме, поворотом осей координат на такой же угол α общее уравнение линии второго порядка может быть приведено к виду

А·х2 + С·у2 + 2·Е·у + 2·D·x + F = 0.

(12.7)

Здесь А·С = 0 и, следовательно, один из коэффициентов А или С равен нулю. Пусть А = 0, С ≠ 0. Представим уравнение (12.7) в виде

или

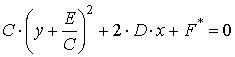
где F * = F – E2. Перенесем начало координат параллельно оси Оу в точку (0, - Е/С), то есть перейдем к новым координатам по формулам х' = х, у' = у + Е/С. Получаем уравнение С·у'2 + 2·D·x' + F* = 0. Если D ≠ 0. Запишем уравнение в виде

.

 Перенесем теперь начало координат параллельно оси Ох' в точку (- F*/2D; 0), перейдем к новым координатам по формулам х'' = х' + F*/2D, у'' = у'. Получаем уравнение С·(у'')2 + 2·D·x'' = 0, или у''2 = 2·p·х'', где введено обозначение р = - D/С. Последнее уравнение является каноническим уравнением параболы.  Если же D = 0, то уравнение имеет вид

С·у'2 + F* = 0.

 Если С и F* имеют разные знаки, то, полагая F* ⁄ C = a2, уравнение можно записать в виде (у' + а)·(y' + a) = 0 Это уравнение определяет пару параллельных прямых.  Если С и F* имеют одинаковые знаки, то уравнение принимает вид у'2 + а2 = 0.Этому уравнению не удовлетворяют координаты никакой точки плоскости. Оно называется уравнением пары мнимых параллельных прямых.  Если F* = 0, то уравнение принимает вид у'2 = 0 и определяет ось О'х'. Это уравнение можно рассматривать как предельный случай при F*→0, то есть как уравнение пары совпадающих прямых. 

36. Функция (отображение, оператор, преобразование) — математическоепонятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значениепеременной   однозначно определяет значение выражения  , а значениемесяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.