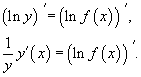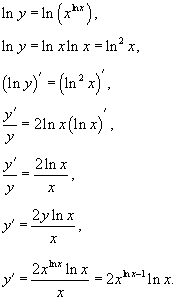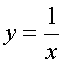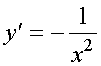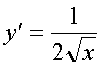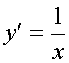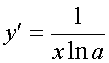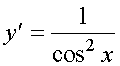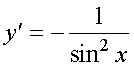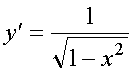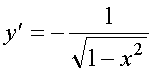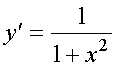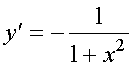55. Производная неявно заданной функции.

Несомненно, в нашем сознании образ функции ассоциируется с равенством и соответствующей ему линией – графиком функции. Например, - функциональная зависимость, графиком которой является квадратичная парабола с вершиной в начале координат и направленными вверх ветвями; - функция синуса, известная своими волнами.

В этих примерах в левой части равенства находится y, а в правой части – выражение, зависящее от аргумента x. Другими словами, имеем уравнение, разрешенное относительно y. Представление функциональной зависимости в виде такого выражения называется явным заданием функции (или функцией в явном виде). И этот тип задания функции является для нас наиболее привычным. В большинстве примеров и задач нам предстают именно явные функции. Про дифференцирование функций одной переменной, заданных в явном виде, мы уже в деталях поговорили.

Однако, функция подразумевает соответствие между множеством значений величины x и множеством значений y, причем это соответствие НЕ обязательно устанавливается какой-либо формулой или аналитическим выражением. То есть, существует множество способов задания функции помимо привычного .

В данной статье мы рассмотрим неявные функции и способы нахождения их производных. В качестве примеров функций, заданных неявно, можно привести или .

Как Вы заметили, неявная функция определяется соотношением . Но не все такие соотношения между x и y задают функцию. Например, ни одна пара действительных чисел x иy не удовлетворяет равенству , следовательно, это соотношение неявную функцию не задает.

может неявно определять закон соответствия между величинами x и y, причем каждому значению аргумента x может соответствовать как одно (в этом случае имеем однозначную функцию) так и несколько значений функции (в этом случае функцию называют многозначной). К примеру, значению x = 1 соответствует два действительных значения y = 2 иy = -2 неявно заданной функции .

Неявную функцию привести к явному виду далеко не всегда возможно, иначе не пришлось бы дифференцировать сами неявные функции. Например, - не преобразовывается к явному виду, а - преобразовывается.

Теперь к делу.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументу x, считая y – функцией от x, и после этого выразить .

Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции. Давайте сразу подробно разберем несколько примеров, чтобы дальше не было вопросов.

Пример.

Продифференцировать выражения по x, считая yфункцией от x.

Решение.

Так как y – это функция от x, то - это сложная функция. Ее можно условно представить как f(g(x)), где f – функция возведения в куб, а g(x) = y. Тогда, по формуле производной сложной функции имеем: .

При дифференцировании второго выражения выносим константу за знак производной и действуем как в предыдущем случае (здесь f – функция синуса, g(x) = y):

Для третьего выражения применяем формулу производной произведения:

Последовательно применяя правила, продифференцируем последнее выражение:

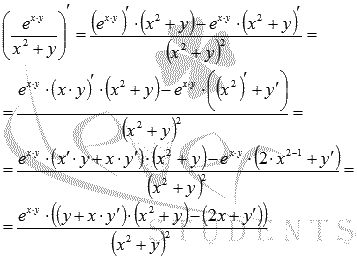
56.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей: