29. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Р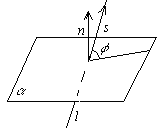 ассмотрим векторы   и  . Если угол между ними острый, то он будет  , где φ – угол между прямой и плоскостью. Тогда  .

Если угол между векторами   и   тупой, то он равен  . Следовательно  . Поэтому в любом случае  . Вспомнив формулу вычисления косинуса угла между векторами, получим  .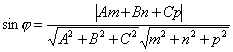

30. Окружность — геометрическое место точек плоскости, удалённых от некоторой точки — центра окружности — на заданное расстояние, называемое радиусом окружности.

Другие определения

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Свойства

Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.

Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).

Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Точка касания двух окружностей лежит на прямой, проходящей через их центры.

Длину дуги окружности радиуса  , образованной центральным углом  , измеренным в радианах, можно вычислить по формуле  .

Длину окружности с радиусом   можно вычислить по формуле  .

Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.

Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.

Угол между двумя секущими, проведёнными из точки, лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.

Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле и дуги напротив неё.

Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.

Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.

Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.

Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.

Окружность является простой плоской кривой второго порядка.

Окружность является коническим сечением и частным случаем эллипса.

Основные формулы

Длина окружности:

Радиус окружности:

Диаметр окружности:

Площадь круга радиуса R:

Площадь сектора, ограниченного углом α, измеряемым в градусах, радиусом R:

Площадь сегмента, ограниченного дугой окружности углом α, хордой:

31. Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек MЕвклидовой плоскости, для которых сумма расстояний до двух данных точек   и   (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

 причем 

Окружность является частным случаем эллипса. Наряду с гиперболойи параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и круговогоцилиндра или как ортогональную проекцию окружности на плоскость.

Свойства

Оптические

Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

Если   и   — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой   равен углу между этой касательной и прямой  .

Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.

Эволютой эллипса является астроида.

Точки пересечения эллипса с осями являются его вершинами.

Эксцентриситет эллипса равен отношению   Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

Эллипс также можно описать как

фигуру, которую можно получить из окружности, применяя аффинное преобразование

ортогональную проекцию окружности на плоскость.

Пересечение плоскости и кругового цилиндра

32. Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от Mдо двух выделенных точек   и   (называемых фокусами) постоянно. Точнее,

 причем 

Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.

33. Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисойпараболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Свойства

Парабола — кривая второго порядка.

Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.

Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

Парабола является антиподерой прямой.

Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.