Семестр 02 / Шпоры по физике 2 сем / Билеты по физике / Билет 4

1. Уравнение состояния газа Ван-дер-Ваальса.

Для описания поведения газов в широком интервале плотностей было предложено много различных уравнений. Самым простым из них и вместе с тем дающим доста­точно хорошие результаты оказалось уравнение Ван-дер-Ваальса. Это уравнение получено путем внесения по­правок в уравнение pV_M=RT (1.63) и имеет следующий вид: где p — давление, оказываемое на газ извне (равное давле­нию газа на стенки сосуда), а и b — константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Поправка a/V_M² характеризует ту добавку к внеш­нему давлению, которая обусловлена взаимным притяже­нием молекул. Заметное воздействие молекул друг на дру­га осуществляется в пределах небольших расстояний, на­зываемых радиусом молекулярного дейст­вия. Поправка b в (1.64) характеризует ту часть объема, которая недоступна для движения молекул. Она равна нескольким суммар­ным объемам молекул, содержащихся в моле газа. Уравнение (1.64) написано для одного моля газа. Чтобы перейти к уравнению для произвольной массы m, нужно учесть, что  молей газа при тех же условиях зани­мают в  раз больший объем: V=V_M. Заменив в (1.64) V_M на V/, получим Умножив это уравнение на  и введя обозначения a=²a, b=b (1.65) приходим к уравнению Ван-дер-Ваальса для  молей Буквами a' и b' обозначены константы Ван-дер-Ваальса для  молей. Их связь с a и b дается соотношениями (1.65). Уравнение Ван-дер-Ваальса в пре­деле, при стремлении объема к бесконечности, переходит в уравнение (1.63).

2. Число ударов молекул газа о стенку сосуда.

Рассмотрим находящийся в равновесии газ, заключен­ный в некотором сосуде. Возьмем элемент поверхности сосуда S и подсчитаем число ударов молекул об этот эле­мент за время t. Выделим из N молекул, заключенных в сосуде, те dN_V молекул, модуль скорости которых лежит в пределах от V до V+dV. Из числа этих молекул направления движения, заключенные внутри телесного угла d. будет иметь количество молекул, равное: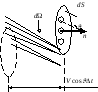

Из выделенных таким образом молекул долетят за время t до площадки S и ударятся о нее молекулы, заключенные в косом ци­линдре с основанием S и высотой 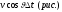Число этих молекул равно 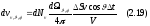(V — объем сосуда). Чтобы получить полное число ула­ров молекул о площадку S, нужно просуммировать вы­ражение (2.19) по телесному углу 2 и по скоростям в пределах от 0 до V_MAX, где V_MAX - наиболь­шая скорость, которой могут обладать молекулы в данных условиях. Начнем с суммирования по направлениям. Для этого представим d в видеи произведем интегрирование выражения (2.19) по в пределах от 0 до /2 и по  в пределах от 0 до 2: Интегрирование по d дает 2, интеграл по равен 1/2. Следовательно, Это выражение дает число ударов о площадку S за время t молекул, летящих в направлениях, заключенных в пределах телесного угла 2, и имеющих модуль скорости от v до v+dv. Суммирование по скоростям дает полное число ударов молекул о площадку S за время t: Выражение представляет собой среднее значение модуля скорости v. Заменив в (2.21) интеграл произведением N<v>, получим

Здесь n=N/V есть число молекул газа в единице объёма. Наконец, разделив выражение (2.22) на S и t, найдём число ударов молекул газа на единицу поверхности стенки в единицу времени: ^.

3. ^{Поверхностное натяжение.}