
Семестр 02 / Шпоры по физике 2 сем / Билеты по физике / Билет 6
.pdf
1. Стоячие волны в струне с 2-мя закрепленными концами
2. Распределения Максвелла.
А) для вектора скорости:
|
|
vx vx , vx |
|
||
v v, v dv vy vy , vy |
||
Т.к. |
|
vz vz , vz |
|
|
|
|
|
|
f(v) (v x ) (v y ) (vz ) f(v)
dvx
dvy
dvz ,то
|
|
m |
2 |
2 |
2 |
||
A exp |
|
|
|
(v x |
v y |
vz ) |
|
2kT |
|||||||
|
|
|
|
|
|
||
Для выяснения способа, которым можно количественно описать распределение молекул по значениям скорости, воспользуемся следующим приѐмом. Возьмем в “воображаемом” пространстве, которое мы будем называть v-пространством (пространством скорости), прямоугольные координатные оси, по которым станем откладывать значения vx, vy и vz отдельных
молекул (имеются в виду компоненты по осям |
x, |
y и z, взятым в обычном |
пространстве). Тогда скорости каждой молекулы будет |
соответствовать точка в |
|
этом пространстве. Из-за столкновений положения точек будут непрерывно |
||
меняться, но их плотность в каждом месте будет оставаться неизменной (т.к. |
||
рассматривается равновесное состояние газа). Вследствии равновесности всех |
||
движений расположение точек относительно начала координат будет сферически |
||
симметричным, следовательно, плотность точек v-пространстве может зависить только от модуля скорости v. Отсюда получаем:
d (v) f (v)4 v dv
2
dVv
F (U ) f (U )4 U 2
|
m |
3 / 2 |
m(U x2 U y2 U z2 ) |
|
|
|
|
|
|
2kT |
2 |
2 |
2 |
|
|||
4a |
|
e |
|
dU x |
U y |
U z |
) |
|
|
|
|||||||
|
2 kT |
|
|
|
|
|
|
|
Б) для модуля скорости:
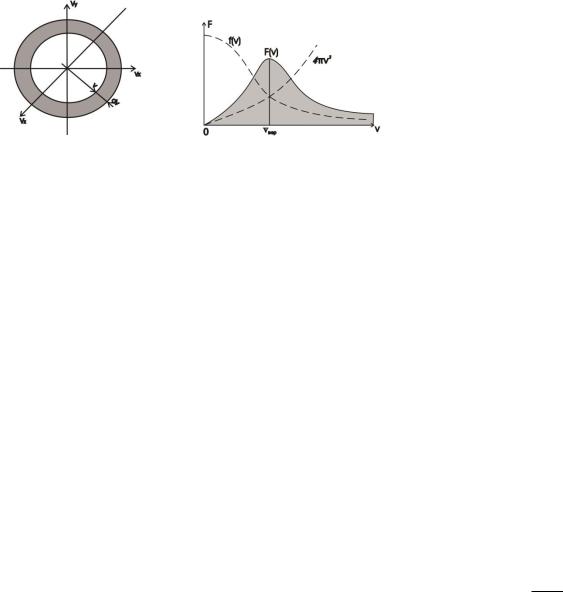
Найдем dw или относительное число молекул, модуль скорости которых заключен в интервале [v, v+dv]. Таким молекулам соответствуют все точки попадающие в шаровой слой с радиусами v и v+dv (рис. 1). Объем этого слоя равен V=4πv2dv. Объемная плотность вероятности во всех точках слоя одинакова, поэтому по теореме о сложении вероятностей, вероятность попадания в этот слой:
dP=f(v)·4πv2dv.
|
|
рис. 1 |
|
|
|
|
|
|
|
|
рис.2 |
|
|
|
|
|
3 |
|
|
|
|
mv2 |
|||
|
|
|
|
m |
|
|
|
|
||||
|
|
|
2 |
|
2 |
|
||||||
F(v)=dP/dv=4πv |
2 |
f(v)→ |
F(v)= 4 |
|
|
v |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
exp |
|
|
|||||||
|
|
|
|
2 kT |
|
|
|
|
2kT |
|||
Это и есть закон распределения Максвелла по модулю скорости. Функция нормирована на единицу, т.е.:
F (v)dv 1
0
3.
Теплоемкость идеального газа при постоянном объеме и при постоянном давлении.
Теплоемкостью какого-либо тела называется величина, равная количеству теплоты, которое нужно
сообщить телу, чтобы повысить его температуру на один кельвин. Аналитически это определение |
|||||||
|
C |
|
|
d Q |
(1.24) |
|
|
записывается следующим образом: |
тела |
dT |
Если нагревание производится при |
||||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
постоянном объеме, то тело не совершает работы над внешними телами и, cледовательно, вся
теплота идет на приращение внутренней энергии тела: d QV=dU. Отсюда следует, что молярная |
|||||
|
C |
dUM |
(V const) |
(1.25) |
|
теплоемкость любого вещества при постоянном объеме равна |
|
В |
|||
V |
dT |
|
|
||
|
|
|
|
|
|
U
термодинамике подобные формулы принято записывать в виде CV M
T
Символ частной
V
производной, снабженный индексом V, указывает на то, что при дифференцировании функции UM по переменной Т объем предполагается постоянным.
Теплоемкость при постоянном давлении Ср бывает больше, чем CV, потому что при p=const нагреваемое тело расширяется и часть подводимой теплоты расходуется на совершение работы над внешними телами.
Внутренняя энергия определяется с точностью до произвольной аддитивной постоянной. Поэтому
константу |
в выражении |
для |
UM |
можно отбросить. В результате получается формула |
||
UM CV T |
(1.27) Внутренняя энергия — величина аддитивная. Следовательно, внутренняя энергий |
|||||
|
|
U |
m |
C T |
(1.28) |
Напишем уравнение d Q=dU + pdV для моля газа, |
массы газа m будет равна |
|
|||||
|
M |
V |
|
|||
предположив, что теплота сообщается газу при постоянном давлении: d QP=dUM + pdVM Разделив это выражение на приращение температуры dT, которое получает газ при сообщении ему теплоты
d QP, придем |
к |
формуле для молярной теплоемкости газа при постоянном |
давлении: |
||||
С |
dUM |
p |
dVM |
( p const) |
|
|
|
|
|
Согласно формуле (1.25) слагаемое dUM/dT равно |
молярной |
||||
P |
dT |
dT |
|
||||
|
|
|
|||||
|
|
|
|
||||
теплоемкости при постоянном объеме. Учтя это и использовав применяемый в термодинамике |
||||
|
|
V |
|
|
|
CP CV p |
M |
|
|
способ записи формул, придѐм к соотношению |
T |
|||
|
P |
|||
|
||||
