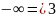- •10. Кольцо многочленов. Теорема о делении с остатком в кольце многочленов над полем.
- •11. Основные понятия теории делимости. Отношение ассоциированности.
- •12. Евклидовы кольца. Евклидовость кольца целых гауссовых чисел.
- •13. Теорема о наибольшем общем делителе в евклидовых кольцах. Алгоритм Евклида.
- •14. Существование и однозначность разложения на неразложимые множители в евклидовых кольцах.
- •15. Поле частных области.
- •22. Поле разложения многочлена.
- •23. Симметрические многочлены. Формулы Виета. Основная теорема о симметрических многочленах.
- •24. Лемма о модуле старшего члена. Основная теорема алгебры комплексных чисел. Классификация неприводимых многочленов над полями комплексных и действительных чисел.
- •25. Последовательность Штурма. Теорема Штурма. Алгоритм построения последовательности Штурма.
25. Последовательность Штурма. Теорема Штурма. Алгоритм построения последовательности Штурма.
Пусть f(x)
[x] без кратных корней.
Последовательность множеств

[x] называется последовательностью Штурма, если выполнены 4 условия:
 не имеет действительных корней.
не имеет действительных корней. не имеют общих действительных корней.
не имеют общих действительных корней.Если
 при 0 <
< s, то
при 0 <
< s, то
 и
и
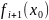 разного знака.
разного знака.Если
 - корень f (т.е.
- корень f (т.е.
 ),
то
),
то
 меняет знак с «-» на «+» при переходе
меняет знак с «-» на «+» при переходе
через .
Пусть есть конечная последовательность
 Вычеркнем из нее 0. Все положительные
числа заменим «+», а все отрицательные
«-». Число мест, где «+» и «-» стоят рядом,
называется числом перемен знаков
в исходной последовательности.
Вычеркнем из нее 0. Все положительные
числа заменим «+», а все отрицательные
«-». Число мест, где «+» и «-» стоят рядом,
называется числом перемен знаков
в исходной последовательности.
-1, 8, 0, 16, -4, 9, 11: -,+, ,+,-,+,+ - 3 перемены знака.
Теорема. Пусть f(x)
[x] без кратных корней и
 [x] – последовательность
Штурма. Для любого c
обозначим через W(c)
число перемен знаков в последовательности
[x] – последовательность
Штурма. Для любого c
обозначим через W(c)
число перемен знаков в последовательности
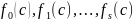 .
Если a,b
и a < b, то
число корней многочлена f(x)
на [a;b] равно
W(a) – W(b).
.
Если a,b
и a < b, то
число корней многочлена f(x)
на [a;b] равно
W(a) – W(b).
|
|
|
|
c-s |
+/- |
+/- |
-/+ |
c |
+/- |
0 |
-/+ |
c+s |
+/- |
+/- |
-/+ |
 .
Рассмотрим 2 случая:
.
Рассмотрим 2 случая:
c – корень при 0 < < s.
Число перемен знаков не меняется при переходе через c.
c – корень

c-s
-/+
+/-
c
0
+/-
c+s
+/-
+/-
Число перемен знаков уменьшится на 1.
Построение последовательности Штурма. Возьмем
в качестве
производную многочлена f.
Если
 уже
уже
определены и deg > 0, поделим на с остатком и положим
равным остатку со знаком «-». .
Проверим, что
.
Проверим, что
 - последовательность Штурма:
- последовательность Штурма:
= НОД(f,f’), он есть ненулевая константа, т.к. многочлен f не имеет кратных корней, а
значит, взаимно прост с f’.
Пусть – общий корень и . Подставим
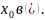 Получим
Получим
 и т.д.
и т.д.
Откуда
 – противоречие.
– противоречие.
П
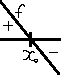 усть
.
Подставим
в (*). Получим
усть
.
Подставим
в (*). Получим
 значит знаки разные.
значит знаки разные.f
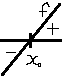 *f’
меняет знак с «-» на «+». f’
> 0 f’ < 0
*f’
меняет знак с «-» на «+». f’
> 0 f’ < 0
Пример. Отделим корни
многочлена

 .
Возьмем в качестве
.
Возьмем в качестве
многочлен
 .
.


|
|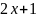
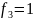
 | x
+ 1
| x
+ 1
 |
|


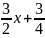
-2x
– 1

|
|
|
1 |
W(c) |
|
- |
+ |
- |
+ |
3 |
|
+ |
+ |
+ |
+ |
0 |
|
- |
0 |
+ |
+ |
1 |
0 ==> 2 |
+ |
+ |
+ |
+ |
0 |
1 ==> |
+ |
- |
- |
+ |
2 |
-1 ==> |
+ |
0 |
- |
+ |
|
-2 ==> |
- |
+ |
- |
+ |
|
-3 ==> |
Вывод. У
три действительных корня:

Пример.
Доказать, что у многочлена
 нет положительных корней.
нет положительных корней.
|
|
|
|
|
+ |
+ |
- |
|
+ |
+ |
- |
 ,
а
- это
,
а
- это
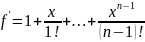 , а в качестве
, а в качестве
 Имеем
Имеем
 В качестве
В качестве
 .
Тогда
.
Тогда
 – последовательность Штурма на [
– последовательность Штурма на [ ]
для любого
]
для любого
 .
.