4.2.Анализ устойчивости исходной сау по критерию Михайлова

Критерий Михайлова основан на рассмотрении кривой, определяемой характеристическим уравнением замкнутой системы.

Если вектор А(jω), характеризующий замкнутую систему регулирования при изменении ω от -ω до +ω описывает в положительном направлении (не изменяя направление) угол равный, то такая система будет устойчива, в противном случае она будет не устойчива.

Для устойчивости системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова, при изменении частоты от 0 до +ω, начинаясь на вещественной положительной полуоси, последовательно обходил против часовой стрелки n квадрантов комплексной плоскости.

Запишем характеристическое уравнение замкнутой САУ

= 0

В характеристическом уравнении заменим оператор s на произведение iω

X(s) = = 5i²ω³· i + 55,1i²ω² + 51,1iω + 43 = (51,1ω – 5ω³)· i + +(43 – 55,1ω²)

Отделяем вещественную часть от мнимой

U(ω) = 43 – 55,1ω²

V(ω) = 51,1ω – 5ω³

Построим годограф Михайлова:

Найдем частоты для построения вектора X(iω):

ω = 0, откуда V(ω) = 0 , U(ω) = 43;

ω = ∞, откуда V(ω) = -∞ , U(ω) = -∞;

Установим точки пересечения кривой с осями абсцисс и ординат, решив уравнения 51,1ω – 5ω³ = 0 и 43 – 55,1ω² = 0 соответственно.

Полученные значения:

ω = 0,88, откуда V(ω) = 41,56, U(ω) = 0;

ω = 3,2, откуда V(ω) = 0, U(ω) = -521,23;

И несколько точек для более точного построения:

ω = 0,5, откуда V(ω) = 24,9 , U(ω) = 29,23;

ω = 1, откуда V(ω) = 46,1 , U(ω) = -12,1;

ω = 1,5, откуда V(ω) = 59,78 , U(ω) = -80,98;

ω = 2, откуда V(ω) = 62,2 , U(ω) = -177,4;

ω = 2,5, откуда V(ω) = 49,63 , U(ω) = -301,38;

ω = 3, откуда V(ω) = 18,3, U(ω) = -452,9.

По рисунку видно, что годограф Михайлова проходит через три квадранта (координатные четверти), что соответствует степени характеристического полинома X(s), то есть система устойчива.

Рис.7. Годограф Михайлова.

5.Анализ качества переходных процессов

Построим график переходных процессов для системы, используя компьютерную программу MATLAB

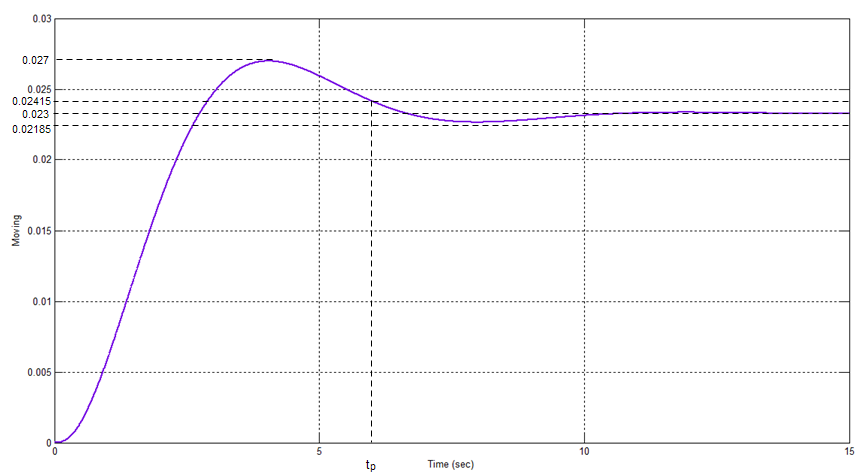
Рис.8. Переходная характеристика САУ.

1)По графику переходных процессов найдем значение перерегулирования (σ):

y_max = 0,027;

y(∞) = 0,023;

.

Следовательно перерегулирование исходной системы при заданных 20% , удовлетворяет должным качествам.

2) По графику переходных процессов найдем время регулирования (t_p):

По графику видно, что характеристическая кривая войдет в канал и больше из него не выйдет, в точке с координатами (6;0.02415). Отсюда получаем, что время регулирования t_p= 6с, но так как это значение больше заданного времени t_p= 0,1с, следовательно по данному показателю качества, переходная характеристика не удовлетворяет необходимым требованиям.

Заключение

По окончанию проделанной работы, можно сделать вывод, что рассмотренная в контрольной работе САУ (система автоматического регулирования температуры воды на выходе теплообменника с паронагревателем), при заданных параметрах, будет являться устойчивой системой автоматического регулирования, но проведя анализ качества переходных процессов, оказалось что время регулирования данной системы, превышает заданное значение. Таким образом можно предположить, что для улучшения показателей качества переходных процессов в САУ, необходимо внести в ее структуру корректирующее устройство.

Список использованной литературы

1.Дорф Р. Бишоп Р. «Современные системы управления»: Пер. с англ. – М.: Лаборатория Базовых Знаний, 2002. – 832с.: ил.

2.Бесекерский В.А., Попов Е.П. «Теория систем автоматического регулирования». – М.: Наука, 1975. – 767 с.

3.«Теория автоматического управления»: Учеб. для вузов. Ч.1. Теория линейных систем автоматического управления / Под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1986. – 367 с.

4.Макаров И.М., Менский Б.М. Линейные автоматические системы. 2-е изд. перераб. и доп.- М.: Машиностроение, 1982. – 536 с.

15