Лабораторная работа 2. Представление чисел в эвм, кодирование

1. Цель работы

Изучить прямой, обратный и дополнительный код, способы кодирования информации. Получить навыки по получению прямого кода, переводу его в обратный, дополнительный и по выполнению арифметических операций с числами, представленными в обратном и дополнительном коде.

2. Теоретический материал

Прямой код. В знаковый разряд помещается цифра знака, а в разряды цифровой части числа — двоичный код его абсолютной величины.

Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями.

Пример: число -1, модуль 0 0000001, обратный код 1 1111110

Пример: число -127, модуль 0 1111111 , обратный код 1 0000000

Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.

число: -1 = дополнительный код 1 1111111

число: -127 = дополнительный код 1 0000001

Сложение обратных кодов

В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительных кодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.

При сложении чисел А и В имеют место четыре случая.

А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

А положительное, B отрицательное и по абсолютной величине больше, чем А.

Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = -7₁₀.

А положительное, B отрицательное и по абсолютной величине меньше, чем А.

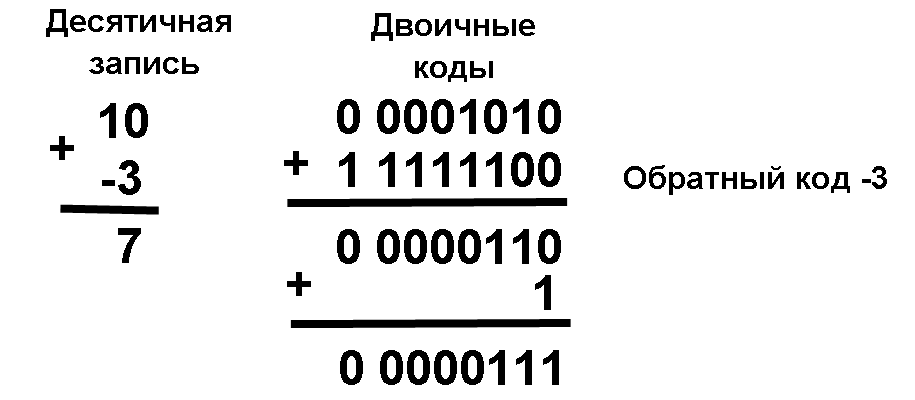
Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.

А и B отрицательные.

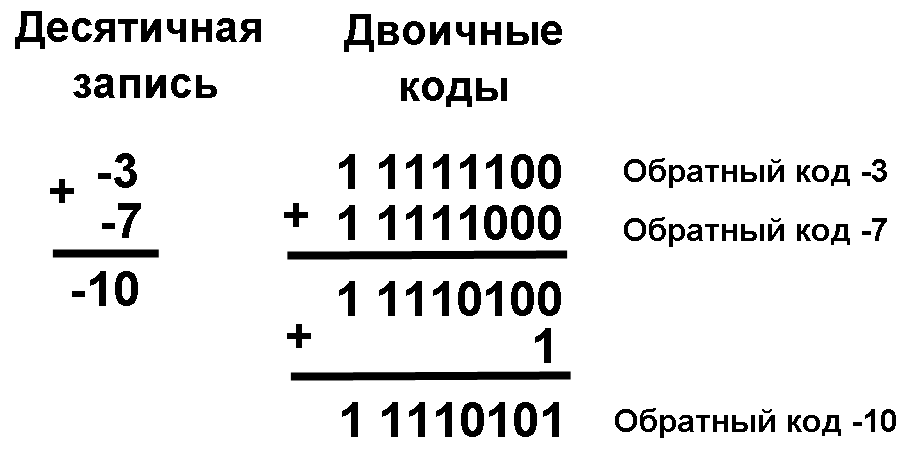
Полученный первоначально неправильный результат (обратный код числа -11₁₀ вместо обратного кода числа -10₁₀) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы. При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = -10₁₀.

При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Случай переполнения возможен и для обратных и для дополнительных кодов.

Сложение дополнительных кодов

А и В положительные.

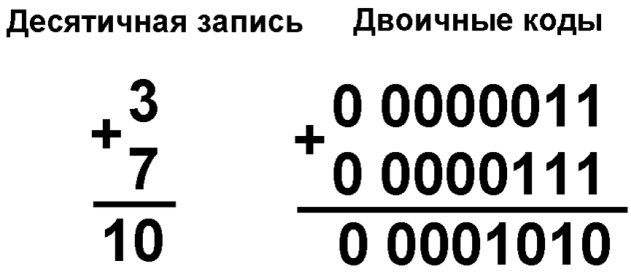
А положительное, B отрицательное и по абсолютной величине больше, чем А.

Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = -7₁₀.

А положительное, B отрицательное и по абсолютной величине меньше, чем А.

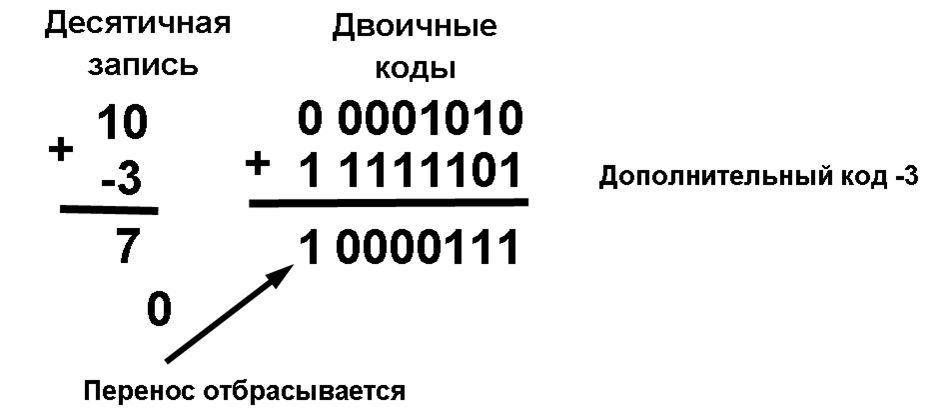
Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

А и B отрицательные.

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.

Арифметические операции с вещественными числами

Сложение. Сложить двоичные нормализованные числа 0.10111 . 2^-1 и 0.11011 . 2¹⁰. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:

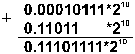
Пример:

X1=0.87654 * 10¹, X2=0.94567*10². Пусть под запись мантиссы отводится 5 разрядов.

1. Δk=1, k₁<k₂ следовательно k₁=k₂=2 (уравняли порядки)

2. мантиссу числа X1 сдвигаем на один разряд влево (пропадет 4)

3. новая мантисса равна 0,94567+0,08765=1,03332

4. мантисса вышла за допустимый интервал >1.

5. нормализуя, получим мантиссу 0,10333 (теряем 2) и порядок увеличиваем на 1.

Ответ: X=0,10333*10^{3 =} 103,3324.

Умножение. Умножение производится по правилу – мантиссы перемножаются, а порядки складываются. Если нужно, то полученное число нормализуется. Пример:

(0.11101*2¹⁰¹)*(0.1001*2¹¹)=(0.11101*0.1001)*2^(101+11)=0.100000101*2¹⁰⁰⁰

Деление. Деление производится по правилу – мантиссы делятся (делимое на делитель), а порядки вычитаются (порядок делителя из порядка делимого). Если нужно, то полученное число нормализуется

0.1111*2¹⁰⁰ : 0.101*2¹¹ = (0.1111 : 0.101)*2^(100-11) = 1.1*2¹ = 0.11*2¹⁰.

Кодирование

Алфавит – множество знаков, в котором определен их порядок (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я)

Источник представляет сообщение в алфавите, который называется первичным, далее это сообщение попадает в устройство, преобразующее и представляющее его во вторичном алфавите.

Код – правило, описывающее соответствие знаков (или их сочетаний) первичного алфавита знаком (их сочетаниями) вторичного алфавита.

Кодирование – перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.

Декодирование – операция обратная кодированию.

Кодер – устройство, обеспечивающее выполнение операции кодирования.

Декодер – устройство, производящее декодирование.

Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечит возврат к исходной информации без каких-либо ее потерь.

Таблица, в которой устанавливается однозначное соответствие между символами и их порядковыми номерами, называется таблицей кодировки.

Для разных типов ЭВМ используют различные таблицы кодировки:

• ANSI - (American National Standards Institute).

• ASCII - (American Standard Cod for Information Interchange).

Таблица кодировки ASCII