2.3.3.Код Грэя

Другой пример последовательности двоичных кодовых слов - это код Грэя. Код Грэя обладает ценным свойством, заключающемся в том, что любые два соседних кодовых слова отличаются лишь значением в одном разряде (последовательность кодовых слов в порядке минимального изменения). Код Грэя используется при построении различных преобразователей аналог-код, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании информации.

Рекурсивное определение двоично-отраженного кода Грея следующее (используются обозначения, введенные в разд.2.3.2):

Примеры последовательностей двоичных наборов в порядке двоичного счета и порядке минимального изменения представлены в таблице 2.1.

Таблица 2.1
Последовательности двоичных наборов в порядке двоичного счета и порядке минимального изменения
Последовательности двоичных наборов в порядке двоичного счета			Последовательности двоичных наборов в порядке минимального изменения (коды Грэя)
G(1)	G(2)	G(3)	G(1)	G(2)	G(3)
0	00	000	0	00	000
1	01	001	1	01	001
	10	010		11	011
	11	011		10	010
		100			110
		101			111
		110			101
		111			100

Рассмотрим алгоритм порождения кода Грэя. Коды Грея удобно задавать начальным словом и последовательностью переходов, т.е. упорядоченным списком номеров разрядов (пронумерованных справа налево, нумерация с единицы), которые меняются при переходе от одного кодового слова к другому. Так для приведенного в таблице 2.1 кода G(3) начальное слово (000), а последовательность переходов будет иметь вид Т₃=1,2,1,3,1,2,1.

Пусть есть последовательность переходов для n-разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.

1) Т₁=1,

2) .

Следует отметить, что последовательности переходов T_n и одинаковы. Поэтому данное рекурсивное определение упрощается:

1) T₁=1,

2) T_n+1=T_n,n+1,T_n.

Итак, для порождения кода Грея достаточно уметь порождать последовательность его переходов.

Последовательность переходов можно порождать итеративно, используя стек. Стек это один из видов организации хранения последовательности элементов данных. Элементы организуются по принципу «последний вошел - первый вышел». Более подробно стеки будут рассмотрены в разд.(2.4.5).

Вначале стек содержит элементы n,n-1,...,1 (с 1 в вершине, т.е. 1 вошла в стек последней). Затем верхний элемент стека - i извлекается из стека и помещается в последовательность переходов, после этого в стек добавляются элементы i-1,i-2,...,1. Процесс повторяется, пока стек не пуст. Алгоритм порождения кода Грея представлен укрупненной блок-схемой на рис.2.5.

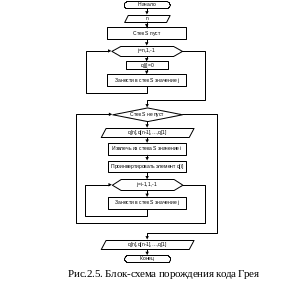
В укрупненной блок схеме не детализировано, как осуществлять операции работы со стеком. Отметим, что для организации стека S можно использовать массив и переменную t, следящую за вершиной стека. Пусть для S отведены ячейки S[1], S[2],...,S[m], и число элементов в стеке не превышает m, тогда пустой стек соответствует случаю t=0. Операции занесения в стек некоторого значения x и извлечения из стека будут осуществляться следующим образом:

• занесение x в стек S: t=t+1; S[t]=x;

• извлечение x из стека S: x:=S[t]; t:=t-1.

Также в укрупненной блок-схеме не детализировано, как выполнять инвертирование элемента q[i]. Заметим, что элемент имеет целочисленный тип, поэтому выполнение операции q[i]:=not q[i] не приведет к желаемому результату (объясните почему). Можно было реализовать операцию инвертирования, например следующим образом: q[i]:=q[i] xor 1 или q[i]:=not q[i] and 1 (объясните почему), но в данном случае лучше заменить инвертирование арифметическими операциями: q[i]:=1-q[i].