
- •Электричество и магнетизм. Лекция 5.
- •Магнитное поле постоянного тока. Закон Био-Савара-Лапласа и его применение для расчета полей.
- •Применение закона Био-Савара-Лапласа для расчета полей:
- •Магнитный поток, теорема Гаусса для магнитного поля.
- •Сила, действующая на проводник с током в магнитном поле.
- •Сила, действующая на заряд, движущийся в магнитном поле.
- •Решение.
- •Работа по перемещению проводника с током в магнитном поле.
Применение закона Био-Савара-Лапласа для расчета полей:
М
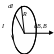 агнитное
поле в центре кругового проводника с
током. Все
элементы кругового проводника с током
создают в центре магнитные поля
одинакового направления – вдоль нормали
от витка.
Поэтому сложение
векторов
можно заменить сложением их модулей.
Т.к. все элементы проводника перпендикулярны
радиусу-вектору
агнитное
поле в центре кругового проводника с
током. Все
элементы кругового проводника с током
создают в центре магнитные поля
одинакового направления – вдоль нормали
от витка.
Поэтому сложение
векторов
можно заменить сложением их модулей.
Т.к. все элементы проводника перпендикулярны
радиусу-вектору
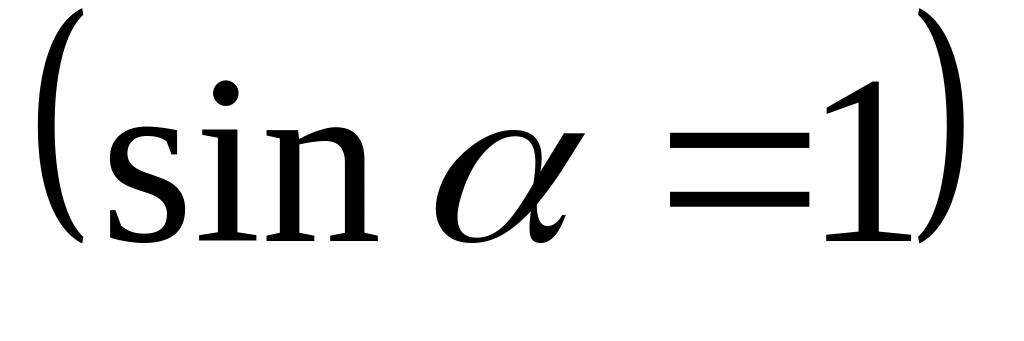 и расстояние всех элементов проводника
до центра кругового тока одинаково и
равно
и расстояние всех элементов проводника
до центра кругового тока одинаково и
равно
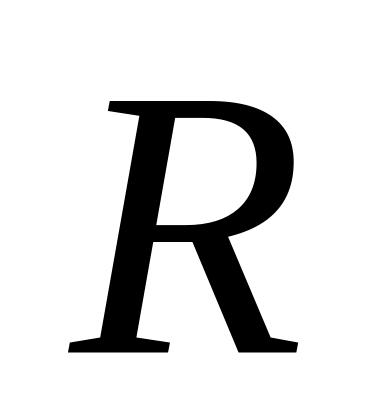 ,
то
,
то
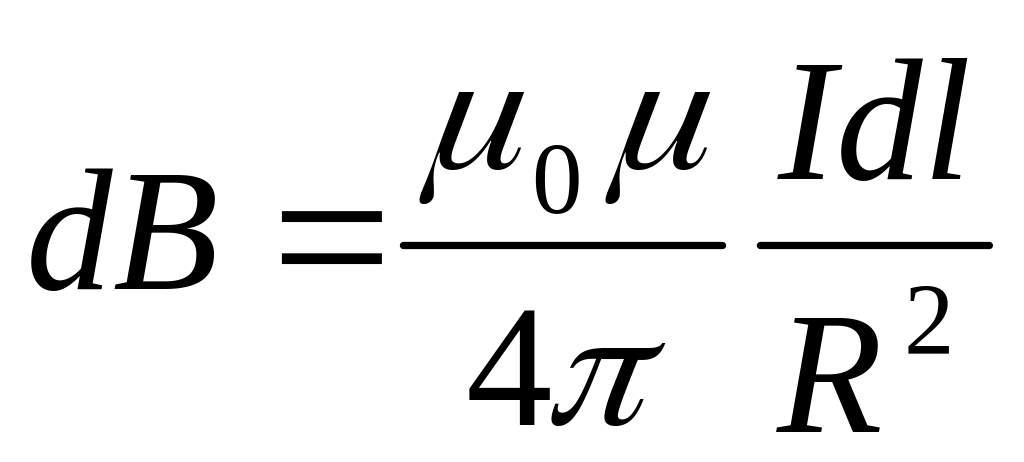 .
Тогда
.
Тогда

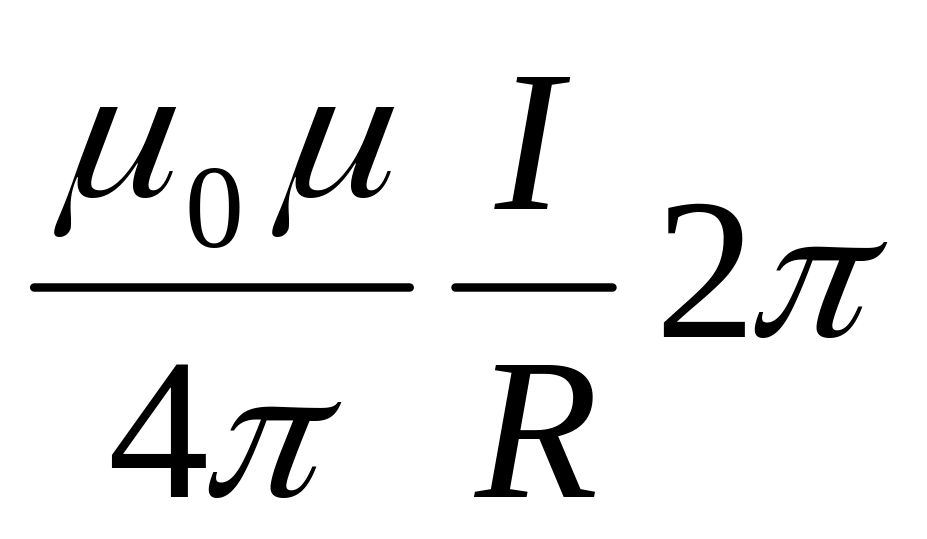 .
Получаем
.
Получаем
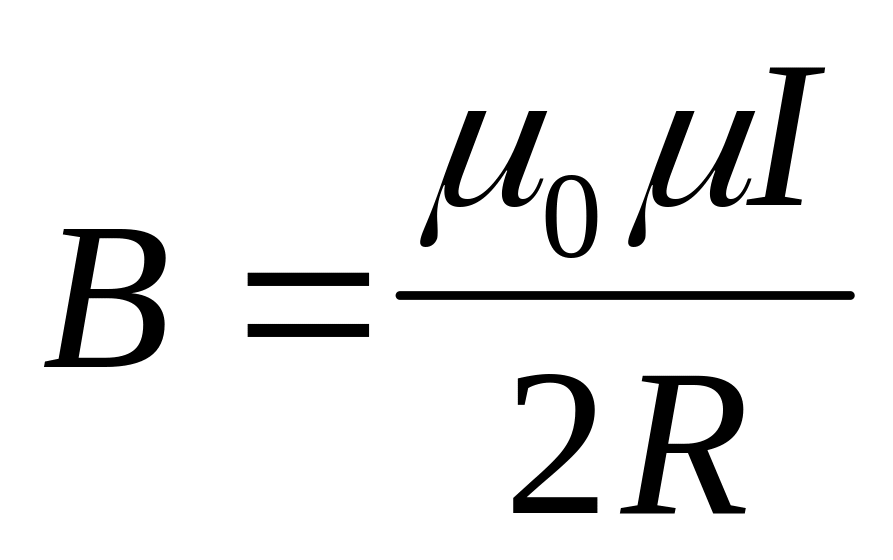 ,
где
,
где
 радиус
кривизны проводника.
радиус
кривизны проводника.
М
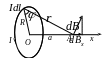 агнитное
поле на оси кругового тока. Выберем
элемент тока
агнитное
поле на оси кругового тока. Выберем
элемент тока
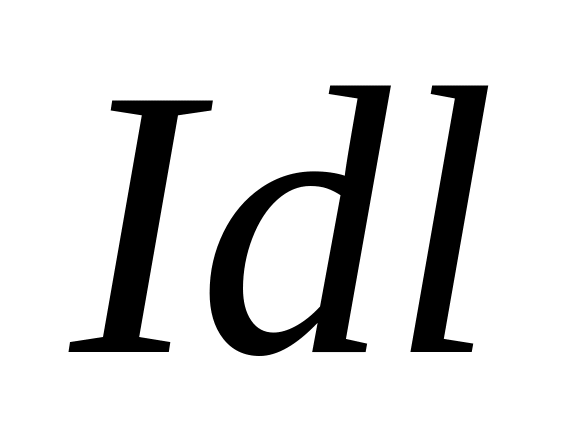 в точке А он создаст поле
в точке А он создаст поле
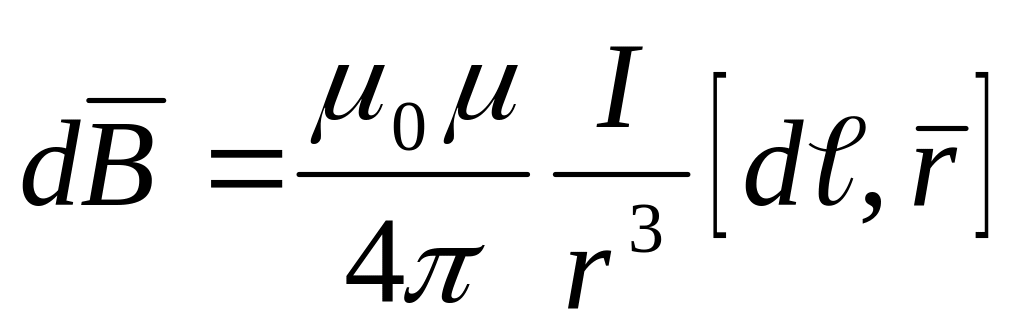 .
В силу симметрии суммарный вектор
.
В силу симметрии суммарный вектор
 направлен вдоль оси
направлен вдоль оси
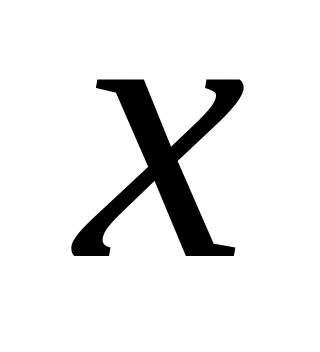 ,
т.е. для нахождения модуля вектора надо
сложить проекции всех векторов
на ось
,
т.е. для нахождения модуля вектора надо
сложить проекции всех векторов
на ось
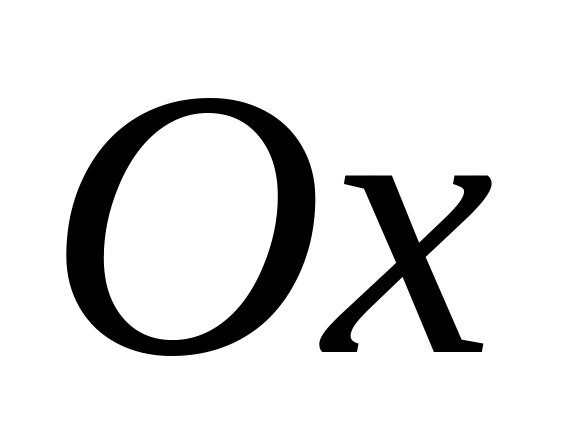 .
.
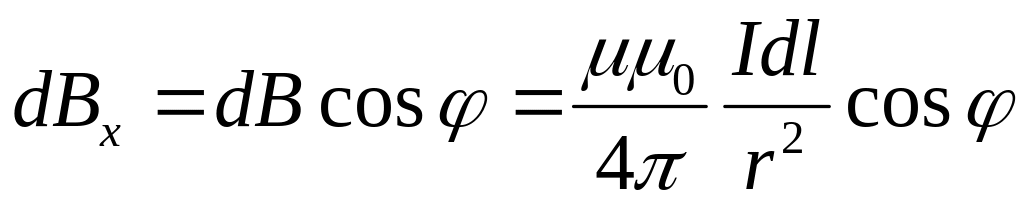 .
Интегрируя это выражение по всем
.
Интегрируя это выражение по всем
 и учитывая, что
и учитывая, что
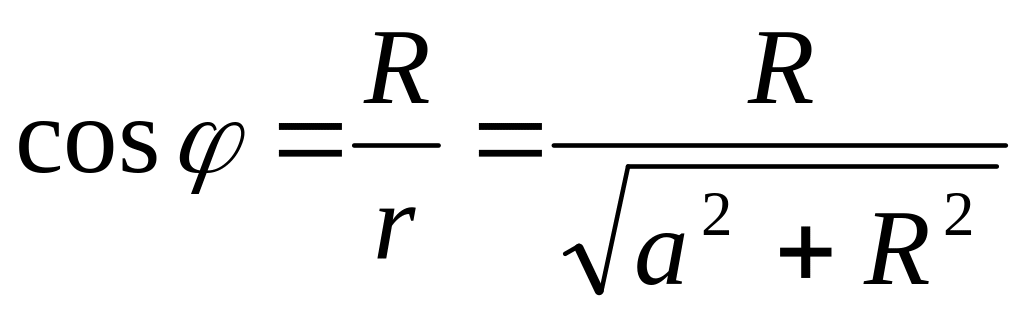 ,
получаем
,
получаем

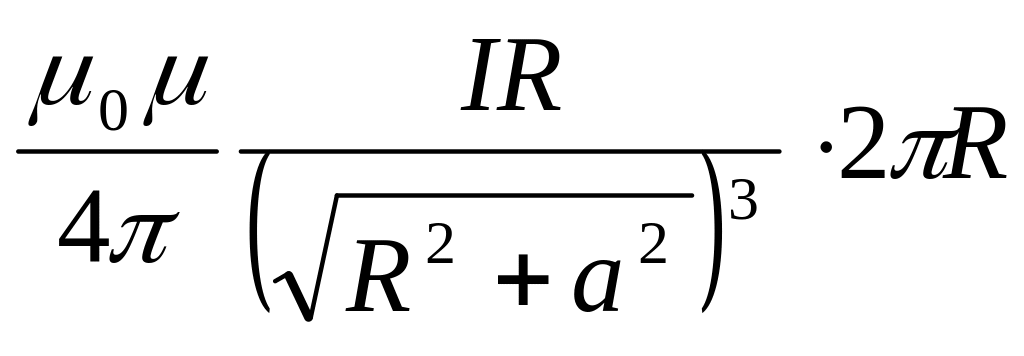 ,
т.е.
,
т.е.
 ,
где
радиус
кругового контура с током,
,
где
радиус
кругового контура с током,
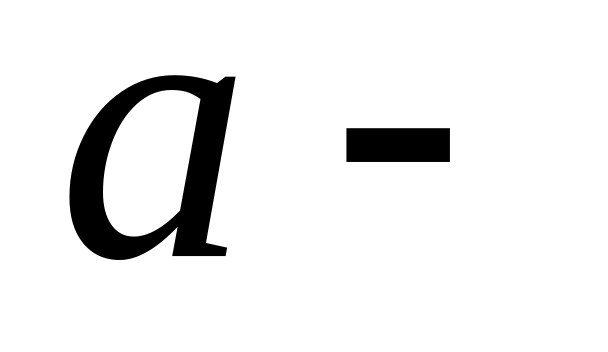 расстояние
от точки, где ищется напряженность, до
плоского контура.
расстояние
от точки, где ищется напряженность, до
плоского контура.М
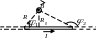
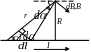 агнитное
поле прямого тока – тока, текущего
по тонкому прямому проводнику бесконечной
длины. В произвольной
точке А, удаленной от оси проводника
на расстояние
,
векторы
от всех элементов тока имеют одинаковое
направление, перпендикулярное плоскости
чертежа («к нам»). Поэтому сложение
векторов
можно заменить сложением их модулей.
В качестве постоянной интегрирования
выберем угол
угол
между векторами
и
,
выразив через него все остальные
величины:
агнитное
поле прямого тока – тока, текущего
по тонкому прямому проводнику бесконечной
длины. В произвольной
точке А, удаленной от оси проводника
на расстояние
,
векторы
от всех элементов тока имеют одинаковое
направление, перпендикулярное плоскости
чертежа («к нам»). Поэтому сложение
векторов
можно заменить сложением их модулей.
В качестве постоянной интегрирования
выберем угол
угол
между векторами
и
,
выразив через него все остальные
величины:
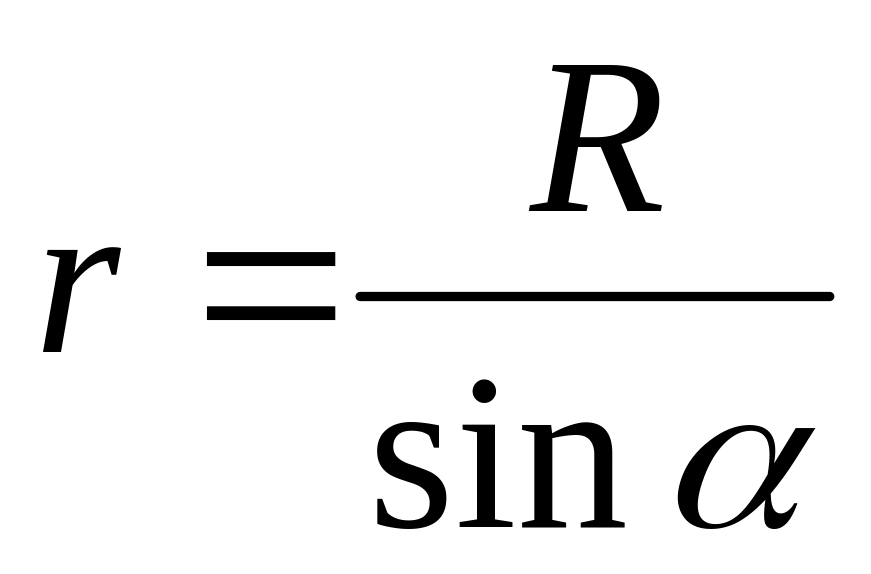 ,
,
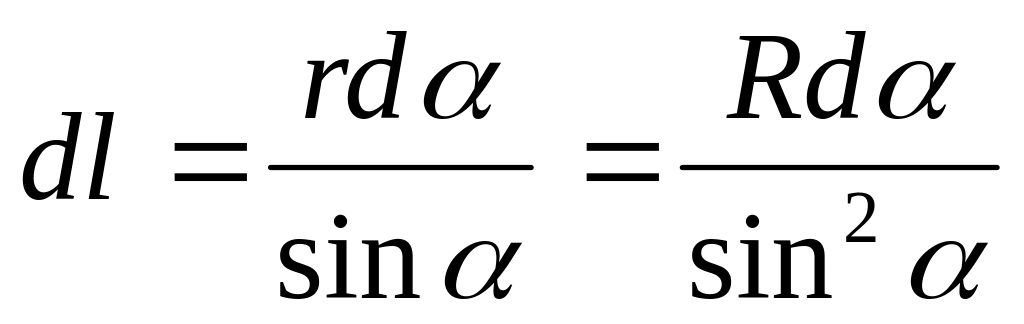 (т.к. угол
(т.к. угол
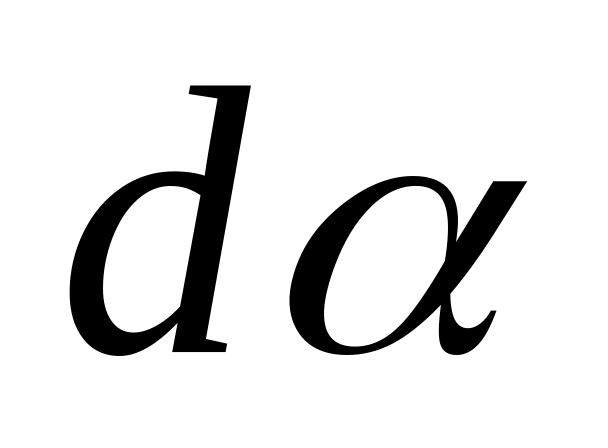 очень мал), получим, что магнитная
индукция, создаваемая одним элементом
проводника, равна
очень мал), получим, что магнитная
индукция, создаваемая одним элементом
проводника, равна
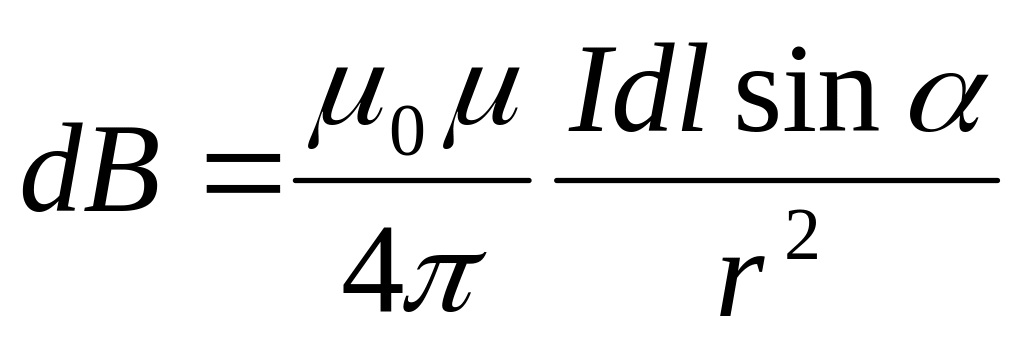

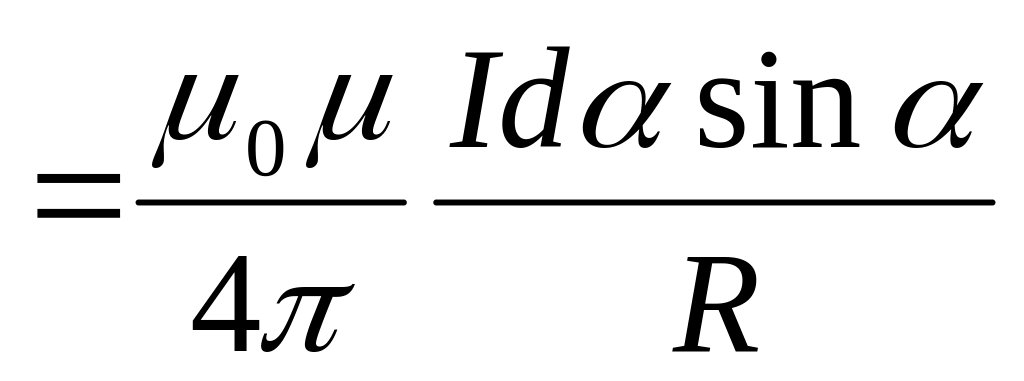 .
Т.к. угол для всех элементов изменяется
в пределах от
.
Т.к. угол для всех элементов изменяется
в пределах от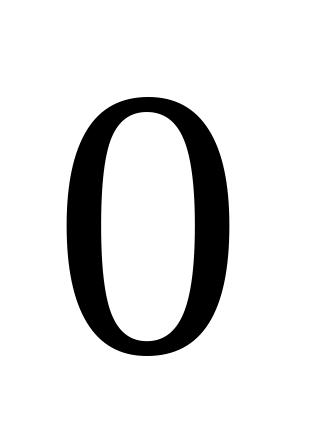 до
до ,
то
,
то
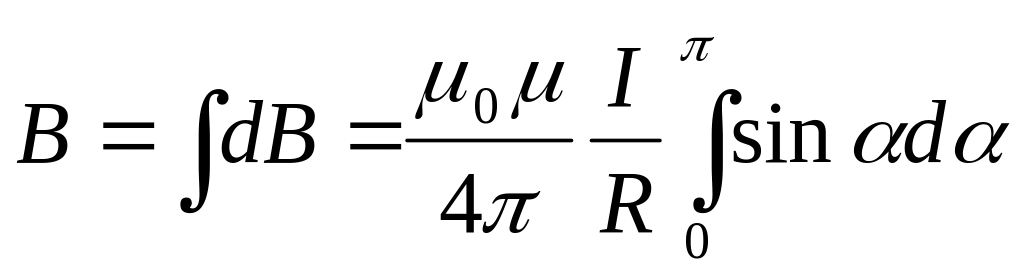
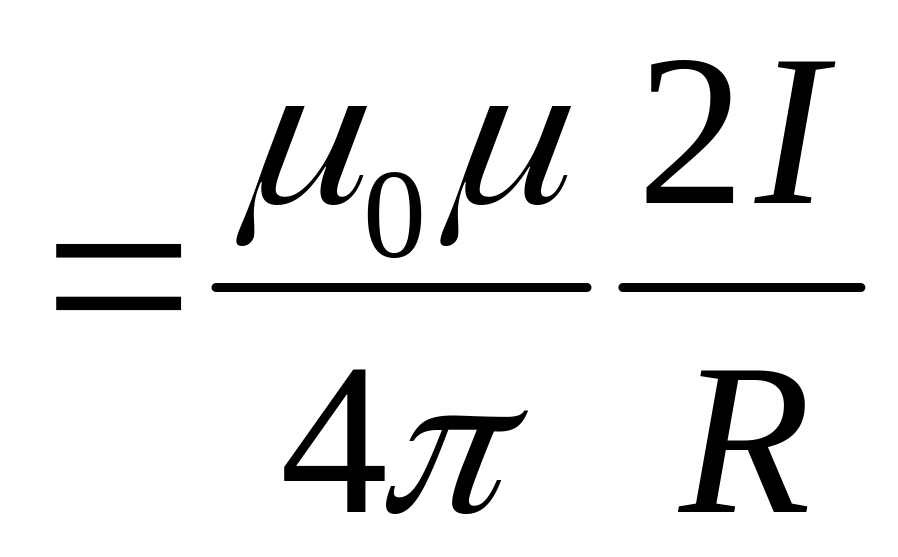 .
Магнитная
индукция
.
Магнитная
индукция
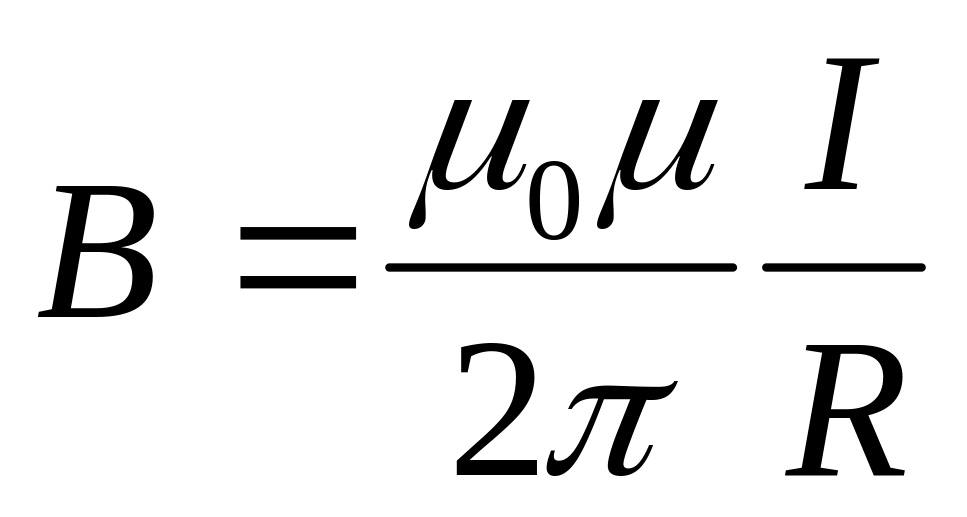 .
.
П ример:
найдем магнитную
индукцию поля, создаваемого отрезком
проводника. По закону Био-Савара-Лапласа
ример:
найдем магнитную
индукцию поля, создаваемого отрезком
проводника. По закону Био-Савара-Лапласа
![]() .
Радиус-вектор направлен от элемента
провода к точке, в которой вычисляется
индукция поля. Выразим длину элемента
проводника
через
.
По чертежу
.
Радиус-вектор направлен от элемента
провода к точке, в которой вычисляется
индукция поля. Выразим длину элемента
проводника
через
.
По чертежу
![]()
![]()
![]() ,
но
величина
переменная, зависящая от
,
но
величина
переменная, зависящая от
![]() :
:
![]()
![]() .
.
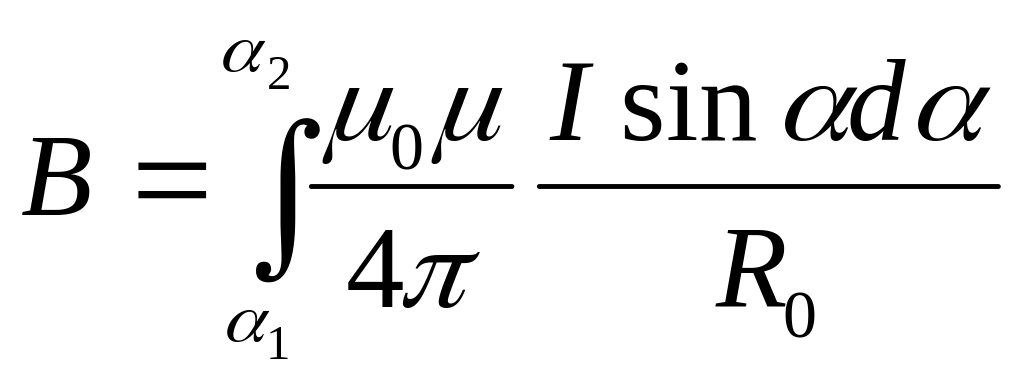
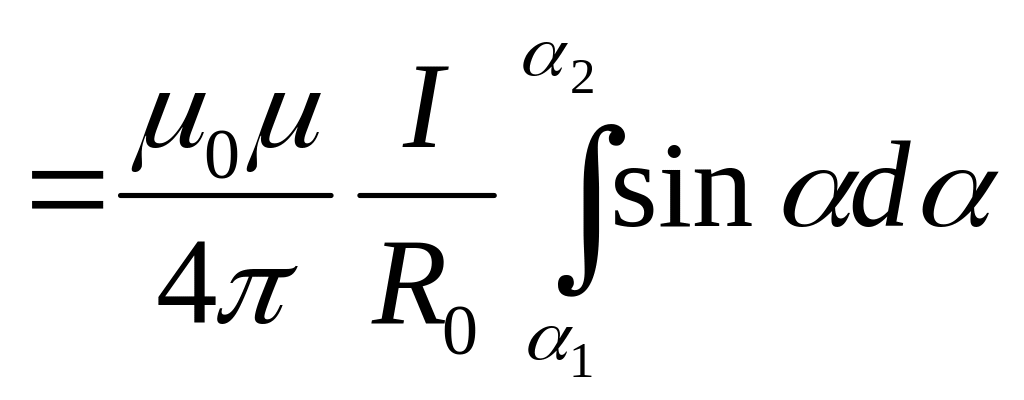 или
или
![]() .
.
П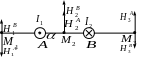 ри
симметричном расположении концов
проводника относительно точки, в которой
определяется магнитная индукция
ри
симметричном расположении концов
проводника относительно точки, в которой
определяется магнитная индукция
![]() и
и
![]()
![]() ,
где
,
где
![]() длина
отрезка проводника.
длина
отрезка проводника.
Пример.
По двум прямолинейным параллельным
противоположно направленным бесконечно
длинным проводникам, находящимся на
расстоянии
![]() ,
текут токи
,
текут токи
![]() и
и
![]() .
Найти напряженность магнитного поля,
вызванного этими токами, в точках
.
Найти напряженность магнитного поля,
вызванного этими токами, в точках
![]() .
Расстояния от проводников до точек
равны:
.
Расстояния от проводников до точек
равны:
![]() ,
,
![]() ,
,
![]() .
Точки лежат на прямой, соединяющей
проводники.
.
Точки лежат на прямой, соединяющей
проводники.
РЕШЕНИЕ.
Согласно принципу суперпозиции
напряженности
![]() ,
,
![]() и
и
![]() магнитного поля в точках
складываются из напряженностей,
создаваемых токами
и
.
магнитного поля в точках
складываются из напряженностей,
создаваемых токами
и
.
![]() ,
,
![]() и
и
![]() .
Напряженность
,
а магнитная индукция проводника
,
тогда
.
Напряженность
,
а магнитная индукция проводника
,
тогда
![]() ,
где
расстояние
от проводника с током до точки, где
определяется напряженность. Тогда
,
где
расстояние
от проводника с током до точки, где
определяется напряженность. Тогда
![]() ,
,
![]() ,
,
![]()
Магнитный поток, теорема Гаусса для магнитного поля.
Потоком вектора
магнитной индукции (магнитным потоком)
через площадку
![]() наз. скалярная величина
наз. скалярная величина
![]() ,
где
угол
между векторами
,
где
угол
между векторами
![]() (вектор
нормали к плоскости контура) и
.
(вектор
нормали к плоскости контура) и
.
Единица: вебер
(Вб).
![]() .
.
Для однородного
поля и плоской поверхности, расположенной
перпендикулярно вектору
:
![]() .
Магнитный поток
.
Магнитный поток
![]() сквозь
поверхность с площадью
сквозь
поверхность с площадью
![]() находится
алгебраическим суммированием потоков
находится
алгебраическим суммированием потоков
![]() сквозь участки поверхности.
сквозь участки поверхности.
Задача 2. В магнитном поле с индукцией 0,1 Т расположен стержень длиной 1 м, который вращается перпендикулярно к направлению линий магнитной индукции. Ось вращения проходит через один из концов стержня. Определить поток магнитной индукции сквозь поверхность, которую образует стержень при каждом обороте.
Д ано:
Решение:
ано:
Решение:
Поток
магнитной индукции при
![]()
![]() равен
,
т.е.
равен
,
т.е.
![]() ,
,
![]()
![]() ,
,
![]()

Ответ:
![]()
Т еорема
Гаусса: поток вектора магнитной
индукции через любую замкнутую поверхность
равен нулю:
еорема
Гаусса: поток вектора магнитной
индукции через любую замкнутую поверхность
равен нулю:
![]() .
.
Э та
теорема отражает факт отсутствия
магнитных зарядов, вследствие чего
линии магнитной индукции не имеют ни
начала, ни конца и являются замкнутыми.
та
теорема отражает факт отсутствия
магнитных зарядов, вследствие чего
линии магнитной индукции не имеют ни
начала, ни конца и являются замкнутыми.
