А) с избыточными связями; б) без избыточных связей.

Поэтому число избыточных связей по формуле (3) будет равно

q=W-Ф=1-1=0.

Заметим, что механизм без избыточных связей можно со­брать без натягов практически при любых первичных ошиб­ках в линейных и угловых параметрах механизма и в этом заключается принципиальное отличие этих механизмов от ме­ханизмов с избыточными связями.

Физический смысл избыточных связей

Рассмотрим неподвижную пространственную кинематиче­скую цепь, нагруженную силой Р (рис. 9,а) для которой

W =0; п =1; р₅=2.

По формулам (4) и (3) найдем

;

q=W-Ф=-0— (—4) =4.

Прове|рим этот результат методом статики. Для этого оп­ределим число N неизвестных реакций в кинематических парах А₅, В_ъ и число V уравнений статики для звена /:

N =2-5=10;

Рис. 9. Кинематические цепи с избыточными связями

Следовательно, число лишних неизвестных (избыточных связей) будет равно 4.

Если в рассмотренном примере изменить относительное расположение кинематических пар, то получим кинематиче­скую цепь, показанную на рис. 9,6", для которой

W=1; p₅ = 2; п = 1. Поэтому по формулам (4) и (3) получим

.

q=W-Ф=1-(-4)=5.

Проверим этот результат методом статики. Число неиз­вестных реакций в кинематических парах равно 2-5 = 10, а уравнений статики для звена / можно написать только пять, так как в одно из уравнений статики ( ) неизвест­ные реакции не входят. Поэтому число лишних неизвестных (избыточных связей) будет равно пяти, т. е., столько, сколь­ко их содержится в одной кинематической паре пятого клас­са. Поэтому в данном случае полученный результат (q=5) можно истолковать иначе: в механизме имеется одна лишняя (избыточная) кинематическая пара, например, пара Вб. Из­быточные кинематические пары называют также пассив­ными кинематическими парами по той причине, что они не влияют на движение звеньев.

Структурная формула для плоских механизмов с избыточными связями

Наибольшее применение в технике получили плоские ме­ханизмы. Любое подвижное звено на плоскости имеет три степени свободы. Поэтому число 3 п обозначает число степе­ней свободы п звеньев плоского механизма до их соедине­ния в кинематические пары.

Каждая низшая пара, независимо от того, является ли она парой 5, 4 или 3-го класса, отнимает у звеньев плоского механизма только две степени свободы. Следова­тельно, все низшие пары отнимут у звеньев 2p_н степеней свободы, где представляет число низших пар.

Каждая высшая пара (второго или первого класса) отни­мет у звеньев плоского механизма только одну степень сво­боды, а все высшие пары отнимут р_а степеней свободы, где р_в — число высших пар.

Таким образом, структурная формула для плоского меха­низма с учетом избыточных связей имеет вид

. (5)

Отсюда найдем число избыточных связей в механизме

, (6)

где для кратности через Ф₃ обозначен многочлен

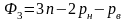(7)

Рассмотрим примеры. Механизм на рис. 10,а имеет сле­дующие параметры:

n =4; p₅ = 6; W₃=1. Вычисляем по формулам (7) и (6):

Проверим этот результат методом статики. Число неизве­стных реакций в шести вращательных кинематических парах равно 2-6=112, а число уравнений статики для четырех звень­ев можно наcчитать в общем случае: 3-4=12. Но в данном случае из-за параллельности звеньев /, 4, 3 одно из уравне­ний статики превращается в тождество вида 0 = 0. Поэтому в механизме получается одна избыточная связь (Сила сжатия или растяжения, например, стержня 4). Если бы стерж­ня 4 не было, то не было бы избыточной связи. Поэтому в данной задаче одна избыточная связь эквивалентна одному избыточному звену (пассивное звено). В общем случае уст­ранение избыточных (пассивных) связей не увеличивает под­вижности механизма.

Схема на рис. 10,6 отличается от предыдущей тем, что звено 4 не параллельно звеньям 1 и 3. Ъ результате получа­ется неподвижная система, для которой

W₃ =0; п=-4; р_и =6.

Для этой системы определим по формулам (7) и (6) Ф₃ = ;

.

Таким образом, данная неподвижная кинематическая цепь не имеет избыточных связей, конечно, при условии, что эта цепь действительно является плоской кинематической цепью, т. е. такой, у которой оси вращательных пар параллельны.

Проверим этот результат методом статики. Число неиз­вестных реакций в системе 2-6=12, а число уравнений стати­ки для четырех звеньев также можно написать 12. Отсюда следует, что число q₃ —0.