Сила, масса, импульс.

Для формулировки II закона Ньютона необходимо ввести понятия массы, силы и импульса.

Известно, что всякое тело противится попыткам изменить его состояние движения.

Опр. 1.2.3. Свойство материальных точек сохранять в случае отсутствия внешних воздействий на них состояние покоя или равномерного прямолинейного движения называют инертностью.

В классической механике:

	Определение		Единицы	Свойства	Примечание
Масса, m	мера инертности тел в поступательном движении. Масса материальной точки равна отношению модулей векторов ее веса Р и ускорения свободного падения g:	скаляр	1кг –масса эталона, хранящегося в Международном бюро мер и весов	масса тела равна арифметической сумме масс всех материальных точек, входящих в состав этого тела:	а) не зависит от скорости движения; 6) масса изолированной системы тел не изменяется при любых происходящих в ней процессах (закон сохранения).
Сила, F	мера механического воздействия на материальную точку или тело со стороны других тел или полей, в результате которого тело изменяет скорость движения или деформируется.	вектор	.	действие на материальную точку нескольких сил экви-валентно действию одной силы, равной векторной сумме этих сил: .	сила полностью задана, если указаны ее численное значение, направление и точка приложения.
Импульс, p	мера движения. Импульсом) материальной точки наз. вектор , равный произведению массы точки на ее скорость .	вектор		импульс системы материальных точек равен геометрической сумме импульсов всех точек системы:	Закон сохранения импульса: импульс замкнутой системы есть величина постоянная:

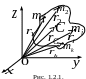
Для вычисления импульса системы материальных точек удобно ввести понятие центра масс.

Опр. 1.2.4. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой определяется радиусом-вектором (1.2.1)

или координатами , , . (1.2.1’)

Тогда импульс системы равен , (1.2.2.) т.е. произведению массы всей системы на скорость одной единственной точки – центра масс.

Для тел массы с непрерывно распределенным веществом (1.2.1”)

П ример 1.2.1. Материальные точки с массой каждая расположены в вершинах треугольника со сторонами 3, 4 и 5м. Найти положение центра масс системы.