Решение:

Имеем . По условию задачи . Отсюда . Подставляя это значение в исходную формулу, получим 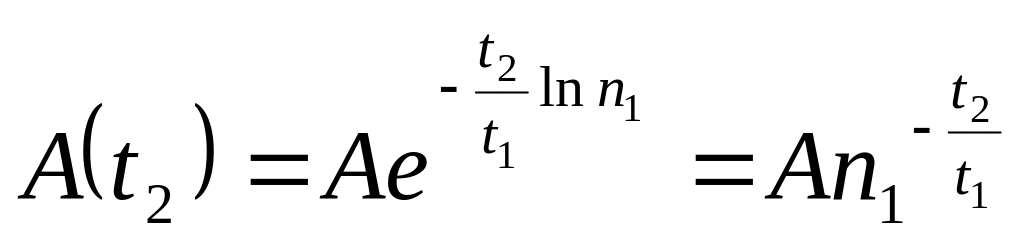. Откуда .

Пример 2.5.2. Тело массой 5г совершает затухающие колебания. Через время тело потеряло 60% своей энергии. Определить коэффициент сопротивления среды.

Решение:

Потеря энергии телом будет равна , откуда или , т.е. . Коэффициент сопротивления среды определяется по формуле .

Пример 2.5.3. Гиря массой 0,5 кг подвешена к пружине, жесткость которой 32 Н/м и совершает затухающие колебания. Определить их период, если 1) за время, в течение которого произошло 88 колебаний, амплитуда уменьшилась в 2 раза; 2) за время двух колебаний амплитуда уменьшилась в 20 раз.

Р Дано: , , ешение:

, собственная циклическая частота . Коэффициент затухания , где находится из уравнения . По условию , . Тогда и , получаем ; . . Решая квадратное уравнение получим и ,

Свободные затухающие колебания (при ) пружинного маятника: сила трения , коэффициент сопротивления. Циклическая частота: . Коэффициент затухания . Добротность .

§6. Апериодическое движение. Вынужденные колебания. Параметрические колебания, автоколебания.

Опр. 2.3.1 При увеличении коэффициента затухания растет период затухающих колебаний и при обращается в бесконечность – движение перестает быть периодическим. При процесс не будет колебательным. Он наз. апериодическим.

Опр. 2.3.2 Автоколебания – незатухающие колебания, поддерживаемые в системе за счет постоянного внешнего источника энергии; свойства колебаний определяются самой системой (часы, двигатели внутреннего сгорания, паровые турбины…).

Любая автоколебательная система состоит из четырех частей:

1. Колебательная система;

2. Источник энергии, компенсирующий потери энергии на затухание колебаний за счет трения или других сил сопротивления;

3. Клапан – устройство, которое регулирует поступление энергии в колебательную систему определенными порциями;

4. Обратная связь – устройство для обратного воздействия автоколебательной системы на клапан, управления работой клапана за счет процессов в самой колебательной системе.

Опр. 2.3.3 Параметрическими наз. колебания, описываемые дифференциальными уравнениями вида

Опр. 2.3.4. Вынужденными наз. колебания системы, вызываемые действием на нее периодических внешних сил. Периодическая сила, вызывающая механические колебания, называется вынуждающей силой.

Примеры вынужденных колебаний: колебания силы тока в электрической цепи, вызываемые переменной э.д.с.; колебания маятника, вызываемые переменной внешней силой.

Дифференциальное уравнение вынужденных колебаний: . В случае механических колебаний , где внешняя вынуждающая сила.

Для пружинного маятника дифференциальное уравнение вынужденных колебаний, происходящих вдоль оси ох под влиянием переменной внешней силы: .

§7. Амплитудные и фазовые резонансные кривые.

Рассмотрим вынужденные колебания пружинного маятника, происходящие под действием вынуждающей силы, которая изменяется по гармоническому закону с циклической частотой : , где амплитуда вынуждающей силы. Амплитуда вынужденных колебаний .

У каждой колебательной системы имеется особая частота, называемая резонансной: . При совпадении частоты вынуждающей силы с резонансной частотой амплитуда вынужденных колебаний достигает максимального значения. Это явление наз. резонансом.

• Н а рисунке 1 – резонансные кривые - зависимость амплитуды вынужденных колебаний от частоты при различных значениях , где .

• Н а рисунке 2 – фазовые резонансные кривые – зависимость сдвига фаз от частоты при различных значениях . .

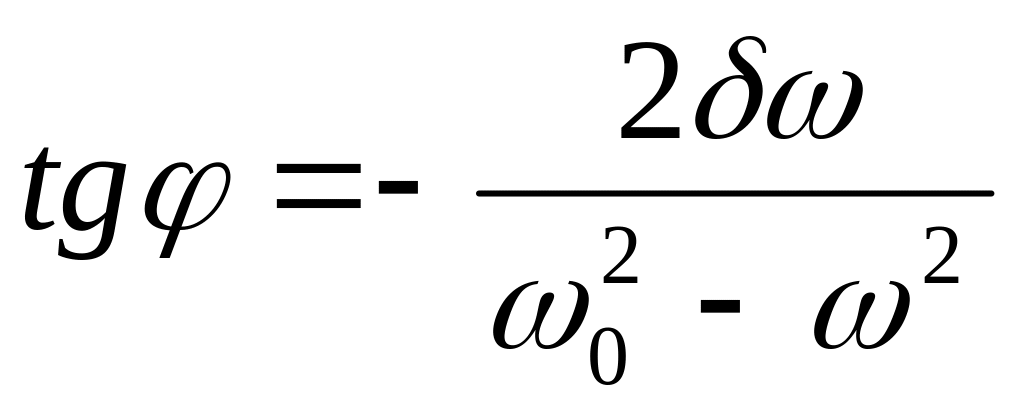Найдем частоту установившихся вынужденных колебаний , при которых амплитуда смещения достигает наибольшего значения.

Работа, совершаемая возмущающей силой за одно полное колебание маятника: , где скорость маятника при установившихся вынужденных колебаниях.

Пример 12.Чему равна амплитуда вынужденных колебаний при резонансе, если при очень малой (по сравнению с собственной) частоте вынужденных колебаний она равна 10см, а логарифмический декремент затухания 0,01?