Р Дано: , ешение:

Т.к. маятники колеблются синхронно, т.е. ,то приведенная длина физического маятника . Приравнивая периоды колебаний маятников, найдем расстояние : , где по теореме Штейнера имеем , . Отсюда , . Подставив численные значения, получим , . Оба значения удовлетворяют условиям задачи, причем .

Пример 2.3.4. На концах тонкого стержня длиной 30 см и массой укреплены грузики массой и . Стержень колеблется около горизонтальной оси, проходящей через его середину. Определить период колебаний, совершаемых стержнем.

Р Дано: , , , ешение:

С тержень – физический маятник, поэтому . Момент инерции данного маятника состоит из моментов инерции обоих грузиков и момента инерции стержня: . Пренебрегая размерами грузиков, получим: , . Момент инерции стержня относительно оси, проходящей через его середину: . Общий момент инерции данного маятника: = . Найдем - расстояние центра тяжести маятника от оси вращения. Напишем условие равновесия стержня с грузиками, находящегося в горизонтальном положении. . Отсюда . Т.о. .

§4. Сложение колебаний.

П од сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система участвует в нескольких колебательных процессах.

Предельные случаи:

1. Одновременно совершаются гармонические колебания одного направления

1. Одинаковой частоты: и , то результирующее колебание совершается с той же частотой по гармоническому закону .

Опр. 2.4.1. Два гармонических колебательных процесса называются когерентными колебаниями, если они согласованно протекают во времени, так что их разность фаз остается постоянной.

Для отыскания и пользуются методом векторных диаграмм, основанный на том, что в каждый момент времени вращающиеся векторы амплитуд складываемых колебаний и результирующий вектор связаны соотношением . В скалярной форме .

Т .к. косинус – функция ограниченная, то возможные значения амплитуды заключе-ны в пределах

Начальная фаза результирующего колебания может быть найдена по формуле: .

Частные случаи:

• , где . Тогда и

• , где . Тогда и

2. Разной частоты: 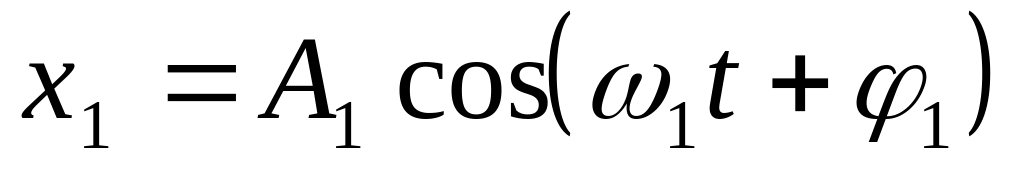и , то результирующее колебание не является гармоническим. Его можно представить в следующей форме: , где .

Начальная фаза . Гармонические колебания, частоты которых различны, некогерентны, т.к. разность их фаз непрерывно изменяется с течением времени.

3. Мало отличаются по частоте – биения. Величина периодически изменяется в пределах от 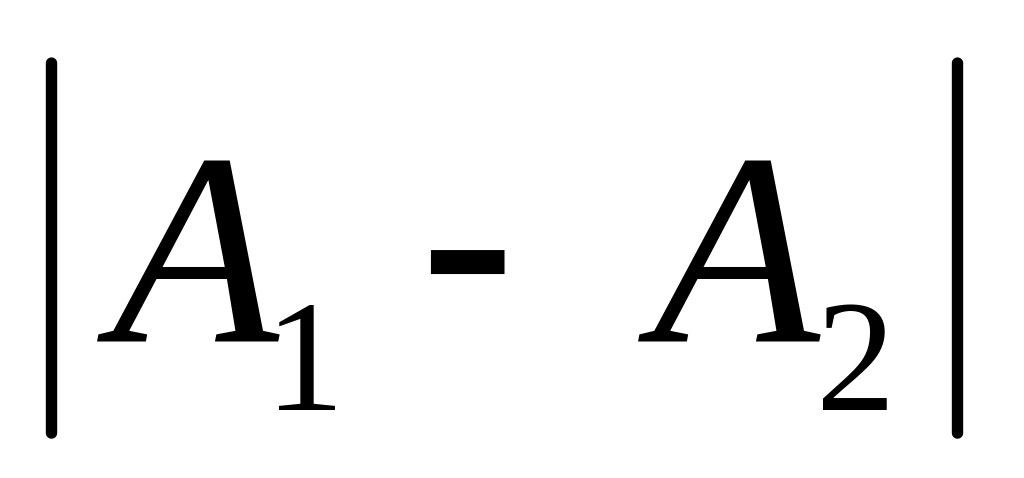до . . Период биения .

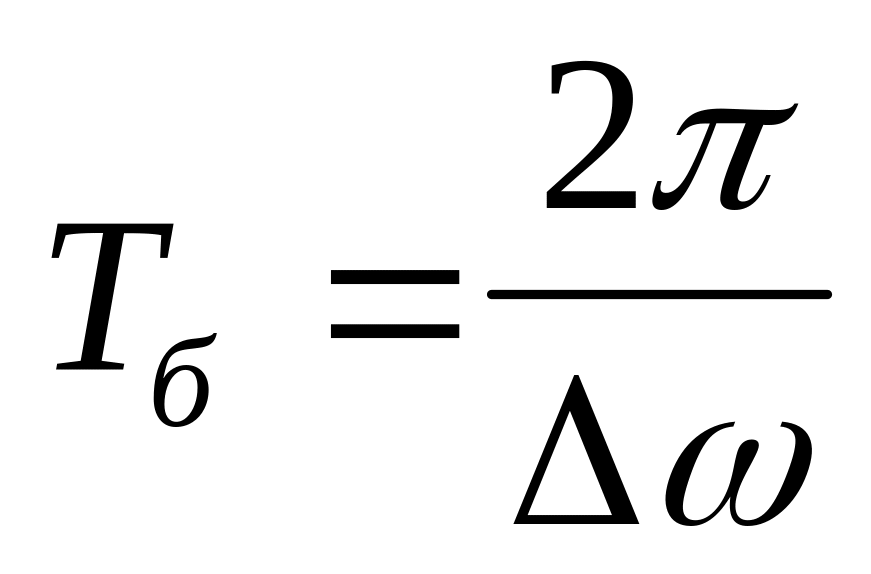Частота биений , возникающих при сложении двух колебаний с различными, но по значению частотами и : .

4. Сложное (негармоническое) периодическое колебание: в виде ряда Фурье.

2. Одновременно совершаются гармонические колебания во взаимно перпендикулярных направлениях вдоль осей x и y.

1. Одинаковой частоты: и 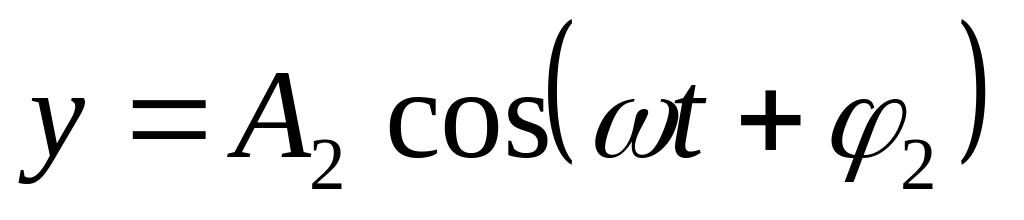. Уравнение траектории результирующего колебания находится с помощью исключения из уравнений параметра t. . Это уравнение эллипса, характеристики которого определяются значением разности фаз 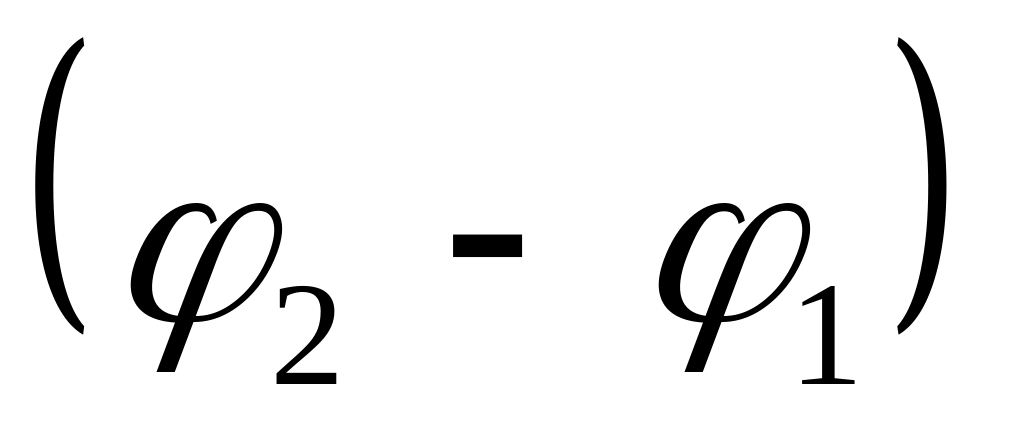. В предельных случаях эллипс вырождается в прямую или окружность. В случае, если начальные фазы , уравнение траектории принимает вид: .

2. Разной частоты: замкнутые траектории, прочерчиваемые точкой называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.

Пример 2.4.1. Совершаются два колебания одинакового направления, выражаемых уравнениями см, и см. Определить амплитуды, периоды и начальные фазы складываемых колебаний. Написать уравнение результирующего колебания.