Р Дано: , , ешение:

Ответ:

П ример 1.4.2. Определить момент инерции тонкого стержня длиной 30 см и массой 200 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.

Найти положение центра масс системы.

Дано:

, ,

Решение:

П

Рис.1.4.11

о теореме Штейнера .

По формуле, полученной в примере 1

для центра тяжести однородного стержня, находим . Рас-

стояние от центра тяжести стержня до заданной оси можно найти по рис.1.4.11, тогда , и

Ответ: .

Пример 1.4.3. Длина одной стороны плоской прямоугольной однородной пластины , масса . Найти момент инерции пластины относительно оси, совпадающей со второй ее стороной.

Дано:

, ,

Решение:

П о формуле 1.4.7. . Т.к. данное тело однородно, т.е. его плотность одинакова по всей плоскости, то .

, и . Получаем .

Ответ:

Пример 1.4.5. Диаметр диска , масса . На расстоянии 10 см от центра диска в плоскости диска находится центр отверстия диаметром . Найти момент инерции полученной фигуры относительно оси, проходящей через центр диска перпендикулярно к его плоскости.

Р Дано: , , , ешение:

(1), где момент инерции сплошного диска; момент инерции вырезанной части. По теореме Штейнера , где момент инерции вырезанной части относительно оси, проходящей через точку О, масса вырезанной части диска,

(2),но , где площадь диска, площадь вырезанной части диска, поверхностная площадь. Подставив в уравнение (2), найдем . Подставив в формулу (1) выражения

и получим .

Ответ:

Уравнение движения твердого тела, вращающегося вокруг неподвижной оси.

Если тело вращается вокруг неподвижной оси, то по (1.4.3.) . Если тело абсолютно твердое, то , т.к. в процессе движения форма и размеры тела не изменяются и , откуда получим выражение, связывающее момент силы и момент инерции: (1.4.10)

- основное уравнение динамики вращательного движения (при описании вращательного движения играет такую же роль, второй закон Ньютона при поступательном).

Выражение (1.4.10) можно получить, если в формуле (1.4.2”) ввести замену .

Из полученного соотношения видно, что момент инерции тела характеризует инерциальные свойства тела при вращательном движении (такие как масса при поступательном). Мы получили, что угловое ускорение таким же образом связано с моментом силы и моментом инерции , каким тангенсальное ускорение связано с силой и массой точки. При таком описании вращательного движения роль силы играет момент силы, роль массы – момент инерции. Т.о., материальные точки с разными массами эквивалентны в смысле приобретаемого ими углового ускорения, если равны их моменты инерции.

а) в общем случае: , (1.4.10)

где момент силы, действующей на тело в течение времени , момент импульса;

б) в случае постоянных момента силы и момента инерции ; (1.4.11)

в) в случае постоянного момента инерции (1.4.12)

г) уравнение динамики тела, вращающегося относительно оси OZ , где и - проекции моментов импульса и внешних сил на ось вращения.

Пример 1.4.6. Тонкий стержень длиной 50 см и массой 400 г вращается с угловым ускорением 3 рад/с² около оси, проходящей через середину стержня перпендикулярно к его длине. Определить вращающий момент М.

Решение: ; ;

П ример 1.4.7. Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?

Решение: Равнодействующая сил и вызывает равноускоренное движение гири ; ; ; ; ; ;

Пример 1.4.8. Вал массой и радиусом вращался с частотой . К цилиндрической поверхности вала прижали тормозную колодку с силой , под действием которой вал остановился через . Определить коэффициент трения.

Решение:

, , , , и .Получаем

Пример 1.4.9. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение оси цилиндра, если цилиндр а) сплошной; б) полый, тонкостенный.

Решение: Равнодействующая сил и вызывает равноускоренное движение цилиндра ; ; ; ;

1) ; ;

2) ;

П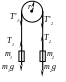 ример 1.4.10. Через блок в виде диска, имеющего массу 80 кг, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами 100 кг и 200 кг. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.