Закон больших чисел.
Теорема.
Пусть
– последовательность независимых
одинаково распределенных случайных
величин (i.i.d.r.v.) с
,
,
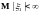и
.
Тогда
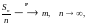
т.е.
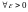
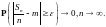
Доказательство. Пусть
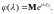
Тогда
фиксированного
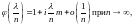
и
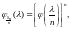
следовательно,
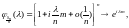
таким образом,
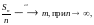
и, следовательно,
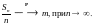
Теорема доказана.
Центральная предельная теорема.
Теорема.
Пусть
– последовательность независимых
одинаково распределенных случайных
величин (i.i.d.r.v.), невырожденных с
,
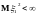и
.
Тогда при
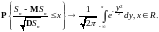
Доказательство.
Пусть
,
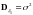и
,
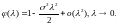
При фиксированном и
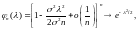
но
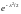– характеристическая функция
,
так как
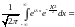
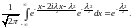
Теорема доказана.
Для вектора
характеристическая функция
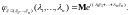
Теорема.
Компоненты вектора
независимы тогда и только тогда, когда
характеристическая функция вектора
равна произведению характеристических
функций его компонент.
Доказательство. Необходимость очевидна. Докажем достаточность.
Пусть
.
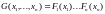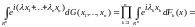
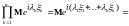
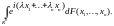
Следовательно,
.
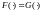Теорема доказана.
Для гауссовского
вектора с плотностью
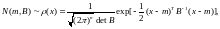
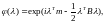
и некоррелированность компонент эквивалентна их независимости.
6. Условные математические ожидания
Условная
вероятность относительно конечного
разбиения
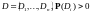
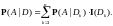
Условная вероятность простой случайной величины
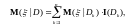
где
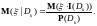
Данная
формула, очевидно, обобщается на случай
произвольной интегрируемой случайной
величины.
Предложение. Для
случайной величины с
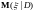– оптимальная в среднеквадратическом
смысле проекция
на
т.е., если
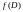– оценка
,
то
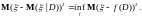
Доказательство.
Для произвольной функции
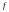
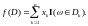
Тогда
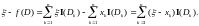
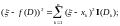
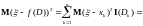
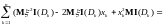
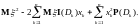
Так как это точка экстремума, то
Следовательно,
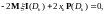
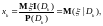
следовательно,
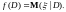
Построим для
-алгебры
(пример
)
.
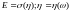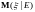Обобщая
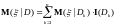
с
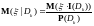
на случай
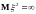(когда нельзя говорить об
)
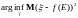введем
Определение.
Условным математическим ожиданием
случайной величины
относительно
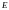называется случайная величина
такая, что
1)
(т.е.
-измерима)
2)
.
О существовании и единственности.
Пусть
.
Определим меру
на
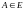следующим образом:
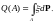
Если
,
то
.
,
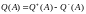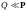следовательно, существует
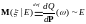
-п.н. единственна так называемая производная Радона-Никодима.
Заметим, что
в том случае, если
,
,
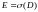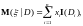
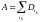то из пункта 2) определения
следует, что
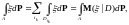
в том числе
при
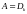
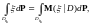
значит
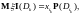
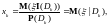
что и обобщает простой случай.
Все свойства условных математических ожиданий в общем случае совпадают со свойствами условных математических ожиданий для простых случайных величин.
Теорема о нормальной корреляции.
Для гауссовского вектора
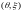оптимальная оценка
вектора
по
и её матрица ошибок
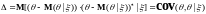
удовлетворяют следующим соотношениям:
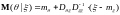
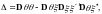
где
,
,
;
;
;
;
.
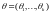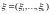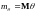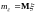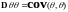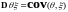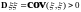Доказательство. Образуем гауссовский вектор
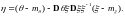
Из того, что
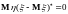следует, что
не коррелирует с
.
Так как
– гауссовский, то и
гауссовский, следовательно,
не зависит от
,
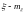значит
;
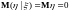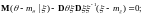
поэтому
;
.
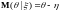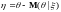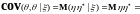
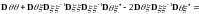
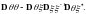
Теорема
доказана.
Следствие. Для
гауссовского вектора
,
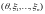где
независимы,
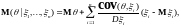
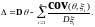
Схема Калмана (частный случай).
На полном
вероятностном пространстве
пусть задан неубывающий поток
-алгебр
,
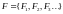т.е.
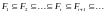и
,
–
-
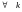
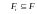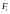алгебра.
Определение.
Последовательность случайных величин
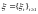называется
-согласованным
случайным процессом, если
–
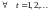
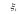- измеримая случайная величина.
Для
упрощения можно предположить, что
.
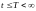Пусть
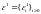и
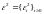– совместно-гауссовские независимые
(и с независимыми по совокупности
компонентами) стандартные случайные
величины. Пусть при каждом
порождается
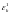и
,
,
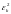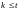т.е.
.
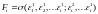Рассмотрим
случайные (очевидно,
-согласованные)
процессы
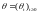и
,
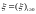определяемые рекурентной формулой:
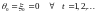
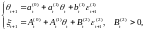
где - доступная наблюдению компонента, а - ненаблюдаема. Задача состоит в построении оценки
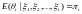
Обозначим
.
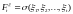Тогда найдем
