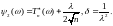- •1. Элементарная теория вероятностей
- •Комбинаторные эксперименты: выборы с возвращением и без, упорядоченные и неупорядоченные.
- •Формула Стирлинга.
- •Свойства вероятности:
- •Свойства условной вероятности:
- •Свойства математических ожиданий
- •Свойства.
- •Следствия:
- •Закон больших чисел я. Бернулли
- •Свойства:
- •Свойства условных математических ожиданий.
- •Задача о разорении.
- •2. Некоторые задачи и определения математической статистики
- •3. Вероятностная модель в общей постановке (в том числе с бесконечным числом исходов)
- •Примеры абсолютно непрерывных распределений
- •4. Математическое ожидание
- •Свойства математических ожиданий.
- •8) Если и , то
- •5. Характеристические функции
- •Свойства:
- •Формулы обращения (обратное преобразование Фурье).
- •Различные виды сходимости.
- •Соотношения сходимостей.
- •Метод характеристических функций.
- •Закон больших чисел.
- •Центральная предельная теорема.
- •6. Условные математические ожидания
- •О существовании и единственности.
- •Теорема о нормальной корреляции.
- •Фильтр Калмана.
- •Некоторые понятия теории случайных процессов.
Свойства:
1)
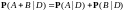 при
2) если
при
2) если
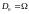 ,
то
,
то
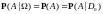 3)
3)
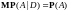 ,
т.е.
,
т.е.
 ,
т.е. формула полной вероятности.
,
т.е. формула полной вероятности.
Пусть
– случайная величина со значениями в
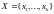 .
.

где
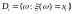 ;
разбиение
;
разбиение
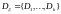 – порождено случайной величиной
.
– порождено случайной величиной
.
Определение.
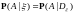 – условная вероятность события
при условии случайной величины
.
– условная вероятность события
при условии случайной величины
.
Заметим, что
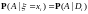 .
.
Аналогично,
если
 – случайные величины,
– случайные величины,
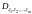 – разбиение порожденное
с атомами
– разбиение порожденное
с атомами
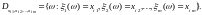
Обозначим
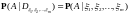 .
.
Определение.
измерима относительно
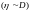 ,
если
,
если
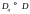
 т.е. если
т.е. если
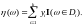
Теорема.
Пусть
– простая случайная величина,
– простая случайная величина и
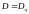 .
Пусть
.
Пусть
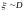 .
.
Тогда
 функция
функция
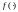 ,
такая, что
,
такая, что
 .
.
Доказательство.
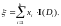
Определим
 для всех различных
для всех различных
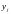 таких, что
таких, что
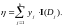
Теорема доказана.
Аналогично,
если
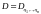 ,
то для любой случайной величины
,
то для любой случайной величины
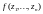 такая, что
такая, что
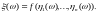
Пусть
– случайная величина на
.
 разбиение
разбиение
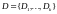 ;
;
 .
.
Определение. Условное математическое ожидание относительно разбиения .

где
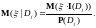
Определение.
 .
.
Свойства условных математических ожиданий.
1)
 2)
2)
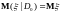 при
3)
при
3)
 4)
4)
 5)
5)
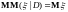 – формула полной вероятности
6) если
– формула полной вероятности
6) если
 ,
то
,
то
 ;
;
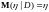 в том числе
в том числе
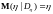 7) если
7) если
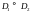 ,
то
,
то
 8) если
и
независимы, то
8) если
и
независимы, то
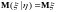 9)
9)
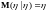 10)
10)

Доказательства свойств 1), 2), 3), 4), 8), 9) очевидны.
Доказательство свойства 5).
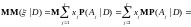
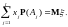
Доказательство свойства 6).
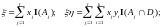
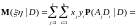
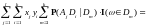
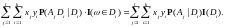
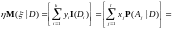

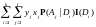
Так как
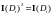 ;
; 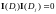 при
при
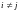 ,
то свойство доказано.
,
то свойство доказано.
Доказательство свойства 7).

следовательно,

Пусть
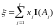 ;
;
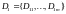 ;
;
 .
.
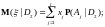
 .
.
Т.е. для доказательства свойства достаточно показать, что справедлива
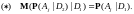
Так как
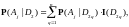
то

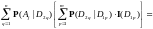
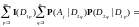
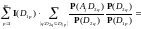
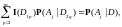
что и
доказывает ( )
.
)
.
Доказательство свойства 10) следует из 7).
Пусть – конечное вероятностное пространство.
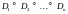 ,
,
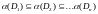 .
.
Определение.
Последовательность случайных величин
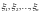 называется мартингалом
относительно потока
называется мартингалом
относительно потока
 ,
если
,
если
1)
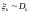
2)
 .
.
Можно
считать, что
 .
Следовательно
.
Следовательно
 .
Пусть
.
Пусть
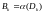 .
.
Определение.
Случайная величина
 со значениями
со значениями
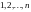 называется моментом остановки
относительно потока
называется моментом остановки
относительно потока
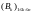
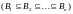 ,
если для любого
,
если для любого
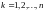 случайная величина
случайная величина

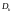 - измерима, т.е.
-
- измерима, т.е.
-
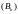 - момент остановки.
- момент остановки.
Пример.
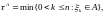
так как
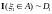 ;
;
 ;
;
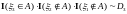 и т.д.
и т.д.
Теорема.
Пусть
 – мартингал и
– некоторый момент остановки относительно
разбиения
– мартингал и
– некоторый момент остановки относительно
разбиения
 .
Тогда
.
Тогда
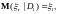
где
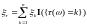
и, следовательно,
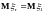 .
.
Доказательство.
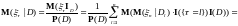
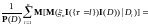
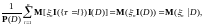
следовательно,
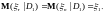
Теорема доказана.
Задача о разорении.
Пусть
–количество денег 1-ого игрока,
– количество денег 2-ого игрока. Введем
последовательность
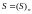 .
.
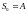 ;
;  ;
;
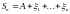 ;
;
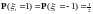 ;
;
 независимы.
Обозначим момент разорения
одного из игроков
:
независимы.
Обозначим момент разорения
одного из игроков
:
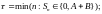
Поскольку
 – мартингал
– мартингал
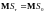 ,
т.е.
,
т.е.
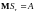 ;
;
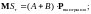
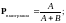
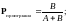
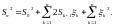
Так как

то

При этом
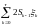 – мартингал, следовательно,
– мартингал, следовательно,
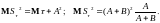
Таким образом
среднее время игры равно
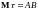 .
.
2. Некоторые задачи и определения математической статистики
Рассмотрим схему серий Бернулли с
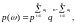
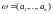 .
.
Пусть
(и
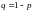 )
– неизвестны заранее, а наблюдаемы
.
Вместо
традиционно используется
)
– неизвестны заранее, а наблюдаемы
.
Вместо
традиционно используется
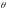 – неизвестный оцениваемый параметр.
Возможны две постановки задачи:
– неизвестный оцениваемый параметр.
Возможны две постановки задачи:
1) задача оценивания;
2) задача построения доверительных интервалов.
Пусть
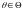 (здесь
(здесь
 ).
).
Следовательно,
задана статистическая модель
 с
с

отвечающая независимым испытаниям.
Всякую
функцию
 назовем оценкой.
назовем оценкой.
Определение.
Оценка
 состоятельна, если
состоятельна, если

Определение. Оценка несмещенная, если

где
 отвечает мере
отвечает мере
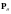 .
.
Определение.
Оценка
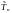 эффективна (в классе несмещенных
оценок
эффективна (в классе несмещенных
оценок
 ),
если
),
если

Пример.
Если
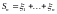 и
и
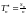 ,
то из закона больших чисел следует, что
,
то из закона больших чисел следует, что

т.е.
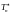 – состоятельная оценка в схеме Бернулли,
– состоятельная оценка в схеме Бернулли,
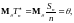
следовательно, – несмещенная. Но любая оценка
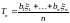
с
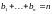 несмещенная, и при
несмещенная, и при
 – состоятельная, а вот эффективна ли
она? Ответ – в так называемом неравенстве
Рао-Крамера.
– состоятельная, а вот эффективна ли
она? Ответ – в так называемом неравенстве
Рао-Крамера.
Теорема. Для несмещенных оценок справедливо неравенство
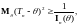
где
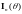 – информация Фишера.
– информация Фишера.
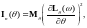
где
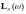 – функция правдоподобия (логарифмическая),
– функция правдоподобия (логарифмическая),
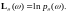
Доказательство.
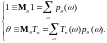
Продифференцируем по :


и, следовательно, по неравенству Коши-Буняковского
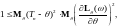
т.е.
где
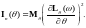
Неравенство доказано (в том числе для общей схемы, не обязательно для схемы Бернулли).
Покажем с помощью неравенства Рао-Крамера, что в схеме Бернулли –эффективная оценка.
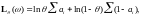
следовательно,
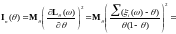
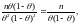
но

следовательно,
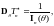
а для всякой другой

следовательно, – эффективна.
Из закона
больших чисел при
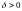
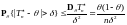
и, следовательно,
для любого
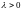
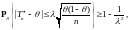
поэтому,
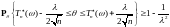
и, следовательно,
Определение.
Интервал вида
 ,
где
,
где
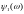 и
и
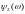 – две функции элементарных событий
называется доверительным интервалом
надежности
– две функции элементарных событий
называется доверительным интервалом
надежности
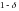 или доверительным интервалом с уровнем
значимости
или доверительным интервалом с уровнем
значимости
 ,
если для любого
,
если для любого
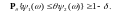
В примере имели место равенства