34 Ошибки выборочного наблюдения. Определение необходимой численности выборки

Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака происходит из-за ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.

Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими. Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. 

На основании теоремы, доказанной П.Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле

– стандартная ошибка.

Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).

Академик A.M. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (Δ), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем:

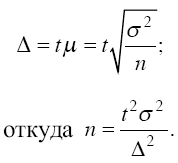
35 Индексы переменного и постоянного состава. Ряды индексов с постоянной и переменной базой, их взаимосвязь

Часто при помощи индексов изучают динамику средних показателей. Изменение средней величины от того или иного показателя зависит: а) от изменения значения каждой отдельной единицы изучаемого явления, б) от изменения структуры явления. (например, средняя цена продажи товара зависит от уровня цен на товар и его удельного веса в объеме продаж; средний рост урожайности зерновых культур зависит от повышения урожайности каждой отдельной культуры и от увеличения ее удельного веса в общей площади более урожайных культур).

Индекс, характеризующий совместное влияние указанных факторов (в котором меняются обе эти величины), называется индексом переменного состава:

,

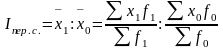где 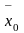- осредненный признак

f- вес (доля) изучаемого признака.

Например, индекс средних цен:

.

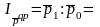
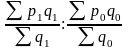Индекс, характеризующий влияние только индексируемой величины (в котором меняется только эта величина), называется индексом постоянного состава:

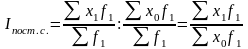
Чтобы изучить влияние изменения структуры на изменение средней величины, исчисляют индекс структурных сдвигов:

,

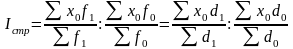где d – доля (удельный вес) продукции в общем объеме.

Взаимосвязь между индексами:

Произведение общих цепных индексов дает базисный индекс последнего периода. Пусть мы имеем 3 периода 1991, 1992, 1993.

.

Эта взаимосвязь имеет место лишь в цепных индексах физического объема (индексах с постоянными весами). В индексах цен, так же и в других индексах с переменными весами, такой взаимосвязи нет.

Отношение последующего базисного индекса к предшествующему равно цепному индексу последующего периода:

.

Поскольку величина объема продукции равна произведению количества продукции на цену, то индекс физического объема (I_q), умноженный на индекс цен (I_p) дает индекс стоимости продукции в фактических ценах (I_qp):

.

Индекс изменения средней величины (I_пер) равен произведению индекса в неизменной структуре (I_пост) на индекс, отображающий влияние изменения структуры явления на динамику средней величины (I_стр):

или .