
- •Статистика как общественная наука. Предмет и метод статистики.
- •3 Понятие корреляционных и функциональных связей. Методы их анализа.
- •Статистическая совокупность. Единица совокупности, ее признаки. Классификация признаков.
- •4 Статистический показатель. Понятие о системе статистических показателей.
- •5 Статистическое наблюдение. Его основные виды и формы, способы проведения.
- •6 Ошибки статистического наблюдения, их определение. Контроль статистических данных.
- •7 Абсолютные величины, их виды, методы измерения и область применения.
- •8 Статистические группировки: понятие, основные этапы проведения, задачи, разновидности группировок.
- •9 Содержание и значение программы статистического наблюдения. План статистического наблюдения, его программно-методологические и организационные вопросы.
- •11 Статистические таблицы: понятие, основные элементы, виды и принципы построения
- •12 Ряды распределения, их виды, принципы построения, приемы графического изображения.
- •13 Относительные величины, их виды, формы выражения и область применения.
- •14 Относительные величины выполнения плана и планового задания. Их связь с относительными величинами динамики.
- •15 Относительные величины динамики. Базисный и цепной способы их расчета.
- •16 Относительные величины интенсивности и координации.
- •17 Относительные величины структуры и сравнения.
- •18 Вариация признаков и причины ее порождающие. Способы определения вариации признаков.
- •19 Средняя арифметическая, ее виды и свойства.
- •20 Особенности исчисления средней арифметической в дискретных и интервальных рядах распределения.
- •22 Средняя гармоническая, ее виды и особенности исчисления.
- •23 Статистические графики: понятие, основные элементы, виды и принципы построения
- •24 Дисперсия, ее свойства и методы расчета. Правило сложения дисперсий.
- •25 Особенности исчисления дисперсии в дискретных и интервальных рядах распределения.
- •26 Понятие и разновидности рядов динамики. Средние показатели ряда динамики.
- •27 Основные элементы индекса.
- •28 Тенденция ряда динамики и методы ее выявления
- •29 Методы изучения сезонных колебаний.
- •30 Понятие об индексах. Индивидуальные и общие индексы. Взаимосвязь индексов.
- •31 Агрегатные индексы. Разложение абсолютного прироста результативного показателя по факторам.
- •32 Понятие выборочного исследования, условия его проведения. Характеристики выборочной совокупности.
- •33 Виды выборки и способы отбора единиц из генеральной совокупности.
- •34 Ошибки выборочного наблюдения. Определение необходимой численности выборки
- •35 Индексы переменного и постоянного состава. Ряды индексов с постоянной и переменной базой, их взаимосвязь
- •36 Ряды динамики. Аналитические показатели ряда динамики.
- •37 Средние индексы. Их связь с агрегатными индексами.
- •38 Понятие функциональных и корреляционных связей. Методы статистического анализа и моделирования связи
- •39 Статистический анализ парной корреляции.
- •40 Статистическая оценка взаимосвязи между качественными признаками с помощью непараметрических методов
- •41 Прогнозирование в рядах динамики на основе экстраполяции.
- •42 Прогнозирование значений результативного признака по уравнению регрессии
- •43 Состав работников предприятия. Показатели численности и движения рабочей силы.
24 Дисперсия, ее свойства и методы расчета. Правило сложения дисперсий.
Дисперсия обладает рядом свойств:
1. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится:
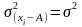 .
.
Если
все значения вариант разделить на
какое-то по постоянное число А, то
дисперсия уменьшится от этого в А2
раз, а среднее квадратическое отклонение
- в А раз: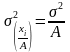 .
.
Если
исчислить дисперсию от любой величины
А, которая отличается от средней
арифметической
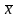 , то эта дисперсия всегда будет больше
дисперсии, исчисленной от средней
арифметической
, то эта дисперсия всегда будет больше
дисперсии, исчисленной от средней
арифметической
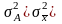 . При этом больше на вполне определенную
величину - квадрат разности между
средней и условно взятой величиной А,
т.е. на
. При этом больше на вполне определенную
величину - квадрат разности между
средней и условно взятой величиной А,
т.е. на
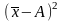 :
:
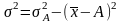 .
.
Исходя из этих свойств, дисперсия для интервального вариационного ряда с равными интервалами определяется по формуле:
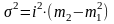 ,
,
где i - величина интервала;
m12 - момент первого порядка в квадрате;
m2- момент второго порядка.
Изучая дисперсию интересующего нас признака, мы не можем определить влияние отдельных факторов, которые характеризуют колеблемость варианта признака. Это можно сделать, разделив изучаемую совокупность на группы, однородные по признаку-фактору, и определив три показателя колеблемости признака в совокупности:
Общая дисперсия – она характеризует вариацию признака, которая зависит от всех условий данной совокупности:
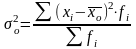 ,
,
где
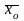 - общая средняя для всей изучаемой
совокупности.
- общая средняя для всей изучаемой
совокупности.
Межгрупповая дисперсия - она отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних около общей средней:
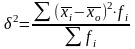 ,
где
,
где
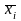 - средняя по отдельным группам;
-
средняя общая; fi
- численность отдельных групп.
- средняя по отдельным группам;
-
средняя общая; fi
- численность отдельных групп.
3. Средняя внутригрупповых дисперсий - характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов и не зависит от признака-фактора, положенного в основу группировки:
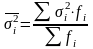 .
.
Правило сложения дисперсий: общая дисперсия равна сумме величин межгрупповой дисперсии и средней из внутригрупповых дисперсий:
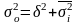 .
.
25 Особенности исчисления дисперсии в дискретных и интервальных рядах распределения.
Дисперсия - средняя арифметическая произведений квадрата отклонений варианта признака xj от среднего арифметического и соответствующих им частот mxj (wxj)
![]() ,
(11)
,
(11)
![]() ,
(12)
,
(12)
где , mxj и wxj определяются по формулам (3), (1) и (2) соответственно.
При вычислении средних величин и дисперсии для интервальных рядов распределения истинные значения признака заменяются центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал.
Исходя из этих свойств, дисперсия для интервального вариационного ряда с равными интервалами определяется по формуле:
,
где i - величина интервала;
m12 - момент первого порядка в квадрате;
m2- момент второго порядка.
