
- •Статистика как общественная наука. Предмет и метод статистики.
- •3 Понятие корреляционных и функциональных связей. Методы их анализа.
- •Статистическая совокупность. Единица совокупности, ее признаки. Классификация признаков.
- •4 Статистический показатель. Понятие о системе статистических показателей.
- •5 Статистическое наблюдение. Его основные виды и формы, способы проведения.
- •6 Ошибки статистического наблюдения, их определение. Контроль статистических данных.
- •7 Абсолютные величины, их виды, методы измерения и область применения.
- •8 Статистические группировки: понятие, основные этапы проведения, задачи, разновидности группировок.
- •9 Содержание и значение программы статистического наблюдения. План статистического наблюдения, его программно-методологические и организационные вопросы.
- •11 Статистические таблицы: понятие, основные элементы, виды и принципы построения
- •12 Ряды распределения, их виды, принципы построения, приемы графического изображения.
- •13 Относительные величины, их виды, формы выражения и область применения.
- •14 Относительные величины выполнения плана и планового задания. Их связь с относительными величинами динамики.
- •15 Относительные величины динамики. Базисный и цепной способы их расчета.
- •16 Относительные величины интенсивности и координации.
- •17 Относительные величины структуры и сравнения.
- •18 Вариация признаков и причины ее порождающие. Способы определения вариации признаков.
- •19 Средняя арифметическая, ее виды и свойства.
- •20 Особенности исчисления средней арифметической в дискретных и интервальных рядах распределения.
- •22 Средняя гармоническая, ее виды и особенности исчисления.
- •23 Статистические графики: понятие, основные элементы, виды и принципы построения
- •24 Дисперсия, ее свойства и методы расчета. Правило сложения дисперсий.
- •25 Особенности исчисления дисперсии в дискретных и интервальных рядах распределения.
- •26 Понятие и разновидности рядов динамики. Средние показатели ряда динамики.
- •27 Основные элементы индекса.
- •28 Тенденция ряда динамики и методы ее выявления
- •29 Методы изучения сезонных колебаний.
- •30 Понятие об индексах. Индивидуальные и общие индексы. Взаимосвязь индексов.
- •31 Агрегатные индексы. Разложение абсолютного прироста результативного показателя по факторам.
- •32 Понятие выборочного исследования, условия его проведения. Характеристики выборочной совокупности.
- •33 Виды выборки и способы отбора единиц из генеральной совокупности.
- •34 Ошибки выборочного наблюдения. Определение необходимой численности выборки
- •35 Индексы переменного и постоянного состава. Ряды индексов с постоянной и переменной базой, их взаимосвязь
- •36 Ряды динамики. Аналитические показатели ряда динамики.
- •37 Средние индексы. Их связь с агрегатными индексами.
- •38 Понятие функциональных и корреляционных связей. Методы статистического анализа и моделирования связи
- •39 Статистический анализ парной корреляции.
- •40 Статистическая оценка взаимосвязи между качественными признаками с помощью непараметрических методов
- •41 Прогнозирование в рядах динамики на основе экстраполяции.
- •42 Прогнозирование значений результативного признака по уравнению регрессии
- •43 Состав работников предприятия. Показатели численности и движения рабочей силы.
19 Средняя арифметическая, ее виды и свойства.
Средняя арифметическая простая
Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:
![]()
Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности
![]()
Средняя арифметическая взвешенная
![]()
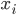 —
цена
за единицу продукции;
—
цена
за единицу продукции;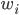 —
количество
(объем) продукции;
—
количество
(объем) продукции;
Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:
1.
Произведение средней на сумму частот
всегда равно сумме произведений вариант
на частоты![]()
2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
![]()
3.Алгебраическая
сумма отклонений индивидуальных
значений признака от средней равна
нулю:![]()
4.Сумма
квадратов отклонений вариантов от
средней меньше, чем сумма квадратов
отклонений от любой другой произвольной
величины ![]() ,
,
![]()
5.
Если все варианты ряда уменьшить или
увеличить на одно и то же число
,
то средняя уменьшится на это же число
:![]()
6.Если
все варианты ряда уменьшить или увеличить
в ![]() раз,
то средняя также уменьшится или
увеличится в
раз:
раз,
то средняя также уменьшится или
увеличится в
раз:
![]()
7.Если
все частоты увеличить/уменьшить в ![]() раз,
то средняя арифметическая не изменится:
раз,
то средняя арифметическая не изменится:![]()
20 Особенности исчисления средней арифметической в дискретных и интервальных рядах распределения.
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах. В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Средняя арифметическая - сумма произведений значений вариантов xj и соответствующих им частот (mxj, wxj), деленная на количество значений признака n.
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
При
расчете средней арифметической для
интервального вариационного ряда
сначала определяют среднюю для каждого
интервала, как полусумму верхней и
нижней границ, а затем — среднюю всего
ряда. В случае открытых интервалов
значение нижнего или верхнего интервала
определяется по величине интервалов,
примыкающих к ним.
Средние,
вычисляемые из интервальных рядов
являются приближенными. Степень их
приближения зависит от того, в какой
мере фактическое распределение единиц
совокупности внутри интервала
приближается к равномерному.
При
расчете средних в качестве весов могут
использоваться не только абсолютные,
но и относительные величины (частость):
![]()
21 Особенности исчисления средней геометрической и средней квадратической величины.
Средняя
геометрическая
величина применяется при расчетах
средних темпов роста для рядов динамики
и имеет следующий вид:
 где П (Х) – произведение, n
- число лет
где П (Х) – произведение, n
- число лет
Средняя квадратическая величина применяется для оценки вариации признака от среднего уровня, при расчете среднего и квадратического отклонения и дисперсии, при расчете коэффициента вариации, при проверке правила сложения дисперсии, в дисперсионном анализе, при расчете моментов в рядах распределения, коэффициентов асимметрии и эксцесса и т.д.
Простая
средняя квадратическая определяется
по формуле:


Взвешенная
средняя квадратическая:
 .
.
